题目内容
【题目】如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上, CE=CA,
AB,CE的延长线交于点F.
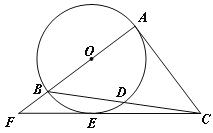
(1)求证:CE与⊙O相切;
(2)若⊙O的半径为3,EF=4,求BD的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OE,OC,通过三角形求得证得∠OEC=∠OAC,从而证得OE⊥CF,即可证得结论;(2)根据勾股定理求得OF,解直角三角形求得tanF=OEEF=34.进而求得AC=6,从而求得△ABC是等腰直角三角形,根据勾股定理求得BC,然后根据等腰三角形三线合一的性质求得DB即可.
解:(1)连接OE,OC.
在△OEC与△OAC中,
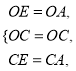
∴△OEC≌△OAC.
∴∠OEC=∠OAC.
∵∠OAC=90°,
∴∠OEC=90°.
∴OE⊥CF于E.
∴CF与⊙O相切.
(2)解:连接AD.
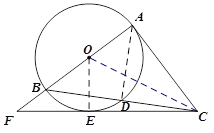
∵∠OEC=90°,
∴∠OEF=90°.
∵⊙O的半径为3,
∴OE=OA=3.
在Rt△OEF中,∠OEF=90°,OE= 3,EF= 4,
∴![]() ,
,
![]() .
.
在Rt△FAC中,∠FAC=90°,![]() ,
,
∴![]() .
.
∵AB为直径,
∴AB=6=AC,∠ADB=90°.
∴BD=![]() .
.
在Rt△ABC中,∠BAC=90°,
∴![]() .
.
∴BD=![]() .
.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目