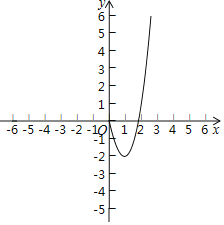ΧβΡΩΡΎ»ί
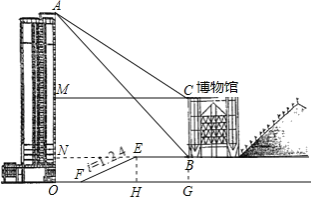
ΓΨΧβΡΩΓΩΓΑ÷Ί«λΉ‘»Μ≤©ΈοΙίΓ±Ήχ¬δ‘ΎΟάάωΒΡγΤ‘Τ…ΫΫ≈œ¬Θ§ΗΟΙίœ÷”–≤ΊΤΖ11Άρ”ύΦΰΘ§ «»ΪΙζ÷––Γ―ß…ζ―–―ß ΒΦυΫΧ”ΐΜυΒΊΘ§Ές¥σΗΫ÷–Ρ≥ ΐ―ß–Υ»Λ–ΓΉιΘ§œκ≤βΝΩ≤©ΈοΙίΒΡΗΏΕ»Θ§ΥϊΟ«œ»‘Ύ≤©ΈοΙί’ΐΕ‘ΟφΒΡ¥σ¬Ξ¬ΞΕΞA¥ΠΘ§≤βΒΟ≤©ΈοΙίΒΉ≤ΩB¥ΠΒΡΗ©Ϋ«ΈΣ50ΓψΘ§≤βΒΟ≤©ΈοΙίΕΞΕΥCΒΡΗ©Ϋ«ΈΣ45ΓψΘ§‘Ό¥”¬ΞΒΉOΨ≠ΙΐΤΫΒΊΒΫ¥οFΘ§‘Ό―ΊΉ≈–±Τ¬œρ…œΒΫ¥οEΘ§ΉνΚσΨ≠ΙΐΤΫΧ®¥οΒΫBΘ§≤βΒΟOFΘΫ20ΟΉΘ§ΤΫΧ®EBΒΡ≥ΛΈΣ28.8ΟΉΘ§“―÷ΣΘ§¬ΞOAΗΏΈΣ60.5ΟΉΘ§–±Τ¬EFΒΡΤ¬Ε»iΘΫ1ΘΚ2.4Θ§AΓΔOΓΔFΓΔEΓΔBΓΔC‘ΎΆ§“ΜΤΫΟφΡΎΘ§‘ρ≤©ΈοΙίΒΡΗΏ‘ΦΈΣ(ΓΓΓΓ)ΟΉΘ°(≤ΈΩΦ ΐΨίΘΚtan50ΓψΓ÷1.2)
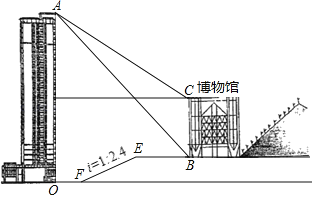
A.10.5B.10.0C.12.0D.12.2
ΓΨ¥πΑΗΓΩB
ΓΨΫβΈωΓΩ
―”≥ΛCBΫΜOFΒΡ―”≥ΛœΏ”ΎGΘ§ΉςEHΓΆOG”ΎHΘ§―”≥ΛEBΫΜOA”ΎNΘ§ΉςCMΓΆOA”ΎMΘ§…η≤©ΈοΙίΒΡΗΏBCΈΣxΟΉΘ§AMΘΫyΟΉΘ§ΗυΨίΤ¬Ε»ΒΡΗ≈Ρν”ΟxΓΔy±μ Ψ≥ωFHΓΔEHΘ§ΗυΨί’ΐ«–ΒΡΕ®“εΝ–≥ωΖΫ≥ΧΘ§ΫβΖΫ≥ΧΒΟΒΫ¥πΑΗΘ°
ΫβΘΚ―”≥ΛCBΫΜOFΒΡ―”≥ΛœΏ”ΎGΘ§ΉςEHΓΆOG”ΎHΘ§―”≥ΛEBΫΜOA”ΎNΘ§ΉςCMΓΆOA”ΎMΘ§
‘ρΥΡ±Ώ–ΈMNBCΈΣΨΊ–ΈΘ§
ΓύMCΘΫOGΘ§MNΘΫBCΘ§
…η≤©ΈοΙίΒΡΗΏBCΈΣxΟΉΘ§AMΘΫyΟΉΘ§
‘ρMNΘΫxΘ§
ΓΏΓœACMΘΫ45ΓψΘ§
ΓύMCΘΫAMΘΫyΘ§
ΓύONΘΫ60.5©¹x©¹yΘ§
‘ρEHΘΫONΘΫ60.5©¹x©¹yΘ§
ΓΏ–±Τ¬EFΒΡΤ¬Ε»iΘΫ1ΘΚ2.4Θ§
ΓύFHΘΫ2.4ΓΝΘ®60.5©¹x©¹yΘ©Θ§
ΓύOGΘΫOF+FH+HGΘΫ20+2.4ΓΝΘ®60.5©¹x©¹yΘ©+28.8ΘΫyΘ§
’ϊάμΒΟΘ§2.4x+3.4yΘΫ194Θ§
‘ΎRtΓςABN÷–Θ§tanΓœABNΘΫ![]() Θ§Φ¥
Θ§Φ¥![]()
’ϊάμΒΟΘ§yΘΫ5xΘ§
Α―yΘΫ5x¥ζ»κ2.4x+3.4yΘΫ194Θ§ΒΟxΘΫ10Θ§Φ¥BCΘΫ10ΟΉΘ§
Ι ―ΓΘΚBΘ°

 ΟΩ»’10Ζ÷÷”ΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
ΟΩ»’10Ζ÷÷”ΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥ΩΈΆβ―ßœΑ–ΓΉιΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§Ε‘Κ· ΐyΘΫx3©¹3xΒΡΆΦœσ”κ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ°«κ≤Ι≥δΆξ’ϊ“‘œ¬ΧΫΥςΙΐ≥ΧΘΚ
(1)Ν–±μΘΚ
x | Γ≠ | ©¹2 |
| ©¹1 |
| 0 |
| 1 |
| 2 | Γ≠ |
y | Γ≠ | ©¹2 | m | 2 |
| 0 |
| n |
| 2 | Γ≠ |
«κ÷±Ϋ”–¥≥ωmΘ§nΒΡ÷ΒΘΜ
(2)ΗυΨί…œ±μ÷–ΒΡ ΐΨίΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒΡΎ≤Ι»ΪΗΟΚ· ΐΒΡΆΦœσΘΜ
(3)»τΚ· ΐyΘΫx3©¹3xΒΡΆΦœσ…œ”–»ΐΗωΒψA(x1Θ§y1)Θ§B(x2Θ§y2)Θ§C(x3Θ§y3)Θ§«“x1ΘΦ©¹2ΘΦx2ΘΦ2ΘΦx3Θ§‘ρy1Θ§y2Θ§y3÷°ΦδΒΡ¥σ–ΓΙΊœΒΈΣΓΓ ΓΓ(”ΟΓΑΘΦΓ±Ν§Ϋ”)ΘΜ
(4)»τΖΫ≥Χx3©¹3xΘΫk”–»ΐΗω≤ΜΆ§ΒΡ Β ΐΗυΘ°«κΗυΨίΚ· ΐΆΦœσΘ§÷±Ϋ”–¥≥ωkΒΡ»Γ÷ΒΖΕΈßΘ°