Question

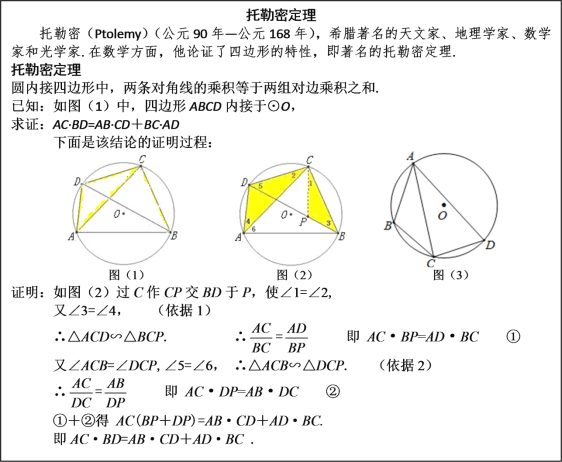
【题目】阅读下列材料，并完成相应的任务.

任务：

（1）上述证明过程中的“依据1”和“依据2”分别指什么？

依据1：

依据2：

（2）当圆内接四边形ABCD是矩形时，托勒密定理就是我们非常熟知的一个定理： （请写出定理名称）.

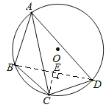
（3）如图（3），四边形ABCD内接于⊙O，AB=3，AD=5，∠BAD=60°，点C是弧BD的中点，求AC的长.

Answer 1

【答案】（1）同弧所对的圆周角相等；两角分别对应相等的两个三角形相似（2）勾股定理（3） AC =

【解析】

（1）根据圆周角定理的推论以及三角形相似的判定定理，即可得到答案；

（2）根据矩形的性质和托勒密定理，即可得到答案；

（3）连接BD，过点C作CE⊥BD于点E．由四边形ABCD内接于⊙O，点C是弧BD的中点，可得BCD是底角为30°的等腰三角形，进而得BD=2 DE=CD，结合托勒密定理，列出方程，即可求解．

（1）依据1指的是：同弧所对的圆周角相等；

依据2指的是：两角分别对应相等的两个三角形相似 ．

故答案是：同弧所对的圆周角相等；两角分别对应相等的两个三角形相似；

（2）∵当圆内接四边形ABCD是矩形时，

∴AC=BD，BC=AD，AB=CD，

∵由托勒密定理得：AC·BD=AB·CD+BC·AD，

∴．

故答案是：勾股定理；

（3）如图，连接BD，过点C作CE⊥BD于点E．

∵四边形ABCD内接于⊙O，

∴∠BAD+∠BCD =180°，

∵∠BAD=60°，

∴∠BCD =120°，

∵点C是弧BD的中点，

∴ 弧BC=弧CD，

∴ BC =CD，

∴∠CBD =30°.

在Rt△CDE中，DE=CD·cos30°，

∴DE=CD ，

∴ BD=2 DE=CD．

由托勒密定理得： AC·BD=AB·CD+BC·AD．

∴AC·CD=3CD+5CD．

∴AC =．