题目内容
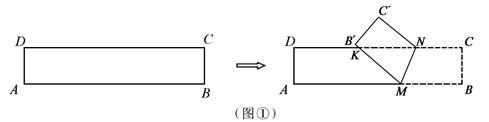
如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD= ,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.
,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.
(1)当点E是AB的中点时,线段DF的长度是 ;
(2)若射线EF经过点C,则AE的长是 .
 ,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.
,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.(1)当点E是AB的中点时,线段DF的长度是 ;
(2)若射线EF经过点C,则AE的长是 .

6;2或5。
(1)如图1,过E点作EG⊥DF,∴EG=AD=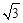 。
。
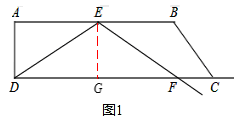
∵E是AB的中点,AB=6,∴DG=AE=3。
∴∠DEG=60°(由三角函数定义可得)。
∵∠DEF=120°,∴∠FEG=60°。
∴tan60°=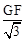 ,解得,GF=3。
,解得,GF=3。
∵EG⊥DF,∠DEG=∠FEG,∴EG是DF的中垂线。∴DF=2 GF=6。
(2)如图2,过点B作BH⊥DC,延长AB至点M,过点C作CF⊥AB于F,则BH=AD=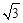 。
。
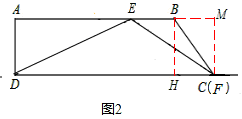
∵∠ABC=120°,AB∥CD,∴∠BCH=60°。
∴CH=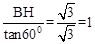 ,BC=
,BC=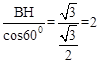 。
。
设AE=x,则BE=6-x,
在Rt△ADE中,DE=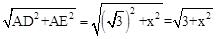 ,
,
在Rt△EFM中,EF= ,
,
∵AB∥CD,∴∠EFD=∠BEC。
∵∠DEF=∠B=120°,∴△EDF∽△BCE。
∴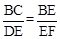 ,即
,即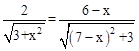 ,解得x=2或5。
,解得x=2或5。
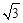 。
。
∵E是AB的中点,AB=6,∴DG=AE=3。
∴∠DEG=60°(由三角函数定义可得)。
∵∠DEF=120°,∴∠FEG=60°。
∴tan60°=
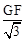 ,解得,GF=3。
,解得,GF=3。∵EG⊥DF,∠DEG=∠FEG,∴EG是DF的中垂线。∴DF=2 GF=6。
(2)如图2,过点B作BH⊥DC,延长AB至点M,过点C作CF⊥AB于F,则BH=AD=
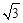 。
。
∵∠ABC=120°,AB∥CD,∴∠BCH=60°。
∴CH=
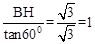 ,BC=
,BC=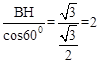 。
。设AE=x,则BE=6-x,
在Rt△ADE中,DE=
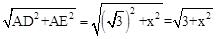 ,
,在Rt△EFM中,EF=
 ,
,∵AB∥CD,∴∠EFD=∠BEC。
∵∠DEF=∠B=120°,∴△EDF∽△BCE。
∴
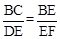 ,即
,即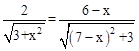 ,解得x=2或5。
,解得x=2或5。
练习册系列答案
相关题目



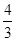 C.
C. D.
D.

 ABCD中,已知点A(﹣1,0),B(2,0),D(0,1).则点C的坐标为 .
ABCD中,已知点A(﹣1,0),B(2,0),D(0,1).则点C的坐标为 .