��Ŀ����
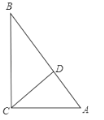
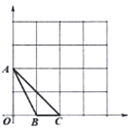
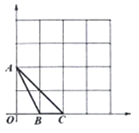
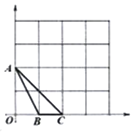
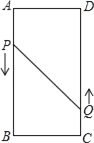
����Ŀ����ͼ��A��B��C��DΪ���ε�4�����㣬AB��16cm��BC��6cm������P��Q�ֱ���3cm/s��2cm/s���ٶȴӵ�A��Cͬʱ��������Q�ӵ�C���D�ƶ���
(1)����P�ӵ�A�ƶ�����Bֹͣ����P��Q�ֱ�ӵ�A��Cͬʱ�������ʾ���2sʱP��Q����֮��ľ����Ƕ���cm��
(2)����P�ӵ�A�ƶ�����Bֹͣ����Q���P��ֹͣ��ֹͣ�ƶ�����P��Q�ֱ�ӵ�A��Cͬʱ�������ʾ����ʱ��P��Q����֮��ľ�����10cm��
(3)����P����AB��BC��CD�ƶ�����P��Q�ֱ�ӵ�A��Cͬʱ��������Q�ӵ�C�ƶ�����Dֹͣʱ����P���Q��ֹͣ��ֹͣ�ƶ�����̽���ʱ���PBQ�����Ϊ12cm2��
���𰸡���1��PQ=6![]() cm����2��
cm����2��![]() s��
s��![]() s����3������4���6����PBQ�����Ϊ 12cm2��
s����3������4���6����PBQ�����Ϊ 12cm2��
��������
���⣨1����PE��CD��E����ʾ��PQ�ij��ȣ�����PE2+EQ2=PQ2�г�������⼴�ɣ�
��2����x���P�͵�Q�ľ�����10cm����Rt��PEQ�У����ݹ��ɶ����г�����x�ķ��̣�16-5x��2=64��ͨ���ⷽ�̼������x��ֵ��
��3���������ۣ�������P��AB��ʱ��������P��BC���ϣ�������P��CD����ʱ��
�����������1������P��PE��CD��E��
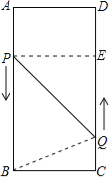
��������⣬��
EQ=16-2��3-2��2=6��cm����PE=AD=6cm��
��Rt��PEQ�У����ݹ��ɶ�������
PE2+EQ2=PQ2����36+36=PQ2��
��PQ=6![]() cm��
cm��
������2sʱP��Q����֮��ľ�����6![]() cm��
cm��
��2����x���P�͵�Q�ľ�����10cm��
��16-2x-3x��2+62=102������16-5x��2=64��
��16-5x=��8��
��x1=![]() ��x2=
��x2=![]() ��
��
������![]() s��
s��![]() sP��Q����֮��ľ�����10cm��
sP��Q����֮��ľ�����10cm��
��3������BQ���辭��ys����PBQ�����Ϊ12cm2��
����0��y��![]() ʱ����PB=16-3y��
ʱ����PB=16-3y��
��![]() PBBC=12����
PBBC=12����![]() ����16-3y����6=12��
����16-3y����6=12��
���y=4��
����![]() ��x��
��x��![]() ʱ��
ʱ��
BP=3y-AB=3y-16��QC=2y����
![]() BPCQ=
BPCQ=![]() ��3y-16����2y=12��
��3y-16����2y=12��
���y1=6��y2=-![]() ����ȥ����
����ȥ����
��![]() ��x��8ʱ��
��x��8ʱ��
QP=CQ-PQ=22-y����
![]() QPCB=
QPCB=![]() ��22-y����6=12��
��22-y����6=12��
���y=18����ȥ����
��������������4���6����PBQ�����Ϊ 12cm2��

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�