题目内容
【题目】已知关于x的方程x2﹣2(a+b)x+c2+2ab=0有两个相等的实数根,其中a、b、c为△ABC的三边长.
(1)试判断△ABC的形状,并说明理由;
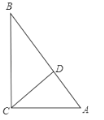
(2)若CD是AB边上的高,AC=2,AD=1,求BD的长.
【答案】(1)见解析;(2)3.
【解析】
(1)根据判别式等于0可得出三边的关系,继而可判断出三角形的形状;
(2)结合(1)的结论,可证△ACD∽△ABC得![]() =
=![]() ,即
,即 ![]() =
=![]() ,解之可得答案.
,解之可得答案.
解:(1)∵两根相等,
∴可得:4(a+b)2﹣4(c2+2ab)=0,
∴a2+b2=c2 ,
∴△ABC是直角三角形;
(2)由(1)可得:△ABC是直角三角形
又∵CD是AB边上的高
∴△ACD∽△ABC
∴![]() =
=![]() ,
,
AC2=AD×AB,
∵AC=2,AD=1,
∴AB=4,
∴BD=AB﹣AD=3.

练习册系列答案
相关题目