ЬтФПФкШн
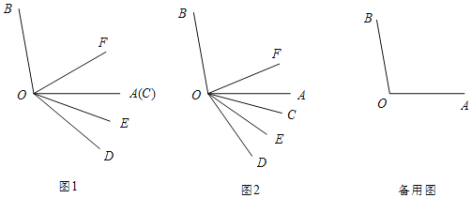
ЁОЬтФПЁПШчЭМввЃЌЁїABCКЭЁїADEЪЧгаЙЋЙВЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=ЁЯDAE=90ЁуЃЌЕуPЮЊЩфЯпBDЃЌCEЕФНЛЕуЃЎ
ЃЈ1ЃЉШчЭММзЃЌНЋЁїADEШЦЕуA а§зЊЃЌЕБCЁЂDЁЂEдкЭЌвЛЬѕжБЯпЩЯЪБЃЌСЌНгBDЁЂBEЃЌдђЯТСаИјГіЕФЫФИіНсТлжаЃЌЦфжае§ШЗЕФЪЧ_____ЃЎ
ЂйBD=CEЂкBDЁЭCEЂлЁЯACE+ЁЯDBC=45ЁуЂмBE2=2ЃЈAD2+AB2ЃЉ
ЃЈ2ЃЉШєAB=4ЃЌAD=2ЃЌАбЁїADEШЦЕуAа§зЊЃЌ
ЂйЕБЁЯEAC=90ЁуЪБЃЌЧѓPBЕФГЄЃЛ
ЂкЧѓа§зЊЙ§ГЬжаЯпЖЮPBГЄЕФзюДѓжЕЃЎ
 ЁЁЁЁ
ЁЁЁЁ ЁЁЁЁЁЁ
ЁЁЁЁЁЁ

ЁОД№АИЁПЂйЂкЂл
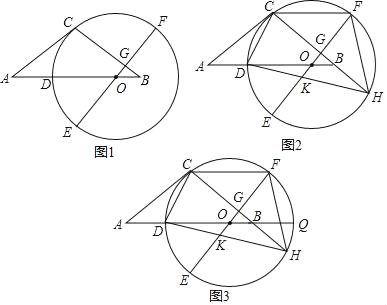
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЂйгЩЬѕМўжЄУїЁїABDЁеЁїACEЃЌОЭПЩвдЕУЕННсТлЃЛЂкгЩЁїABDЁеЁїACEОЭПЩвдЕУГіЁЯABD=ЁЯACEЃЌОЭПЩвдЕУГіЁЯBDC=90ЁуЖјЕУГіНсТлЃЛЂлгЩЬѕМўжЊЁЯABC=ЁЯABD+ЁЯDBC=45ЁуЃЌгЩЁЯDBC+ЁЯACE=90ЁуЃЌОЭПЩвдЕУГіНсТлЃЛЂмЁїBDEЮЊжБНЧШ§НЧаЮОЭПЩвдЕУГіBE=BD+DEЃЌгЩЁїDAEКЭЁїBACЪЧЕШбќжБНЧШ§НЧаЮОЭгаDE=2ADЃЌBC=2ABЃЌОЭгаBC=BD+CD2ЁйBDОЭПЩвдЕУГіНсТлЃЎЃЈ2ЃЉЂйЗжСНжжЧщаЮaЁЂШчЭМ2жаЃЌЕБЕуEдкABЩЯЪБЃЌBE=AB-AE=1ЃЎгЩЁїPEBЁзЁїAECЃЌЕУ![]() ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЎbЁЂШчЭМ3жаЃЌЕБЕуEдкBAбгГЄЯпЩЯЪБЃЌBE=3ЃЎНтЗЈРрЫЦЃЎЂкШчЭМ5жаЃЌвдAЮЊдВаФADЮЊАыОЖЛдВЃЌЕБCEдкAЩЯЗНгыAЯрЧаЪБЃЌPBЕФжЕзюДѓЃЎЧѓГіPBМДПЩЃЎ
ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЎbЁЂШчЭМ3жаЃЌЕБЕуEдкBAбгГЄЯпЩЯЪБЃЌBE=3ЃЎНтЗЈРрЫЦЃЎЂкШчЭМ5жаЃЌвдAЮЊдВаФADЮЊАыОЖЛдВЃЌЕБCEдкAЩЯЗНгыAЯрЧаЪБЃЌPBЕФжЕзюДѓЃЎЧѓГіPBМДПЩЃЎ
ЯъНтЃКЃЈ1ЃЉНтЃКШчЭММзЃК

ЂйЁпЁЯBAC=ЁЯDAE=90ЁуЃЌ
ЁрЁЯBAC+ЁЯDAC=ЁЯDAE+ЁЯDACЃЌ
МДЁЯBAD=ЁЯCAEЃЎ
дкЁїABDКЭЁїACEжаЃЌ
AD=AFЃЌЁЯBAD=ЁЯCAEЃЌAB=ACЃЌ
ЁрЁїABDЁеЁїACEЃЈSASЃЉЃЌ
ЁрBD=CEЃЌЁрЂйе§ШЗЃЛ
ЂкЁпЁїABDЁеЁїACEЃЌ
ЁрЁЯABD=ЁЯACEЃЎ
ЁпЁЯCAB=90ЁуЃЌ
ЁрЁЯABD+ЁЯAFB=90ЁуЃЌ
ЁрЁЯACE+ЁЯAFB=90ЁуЃЎ
ЁпЁЯDFC=ЁЯAFBЃЌ
ЁрЁЯACE+ЁЯDFC=90ЁуЃЌ
ЁрЁЯFDC=90ЁуЃЎ
ЁрBDЁЭCEЃЌЁрЂке§ШЗЃЛ
ЂлЁпЁЯBAC=90ЁуЃЌAB=ACЃЌ
ЁрЁЯABC=45ЁуЃЌ
ЁрЁЯABD+ЁЯDBC=45ЁуЃЎ
ЁрЁЯACE+ЁЯDBC=45ЁуЃЌЁрЂле§ШЗЃЛ
ЂмЁпBDЁЭCEЃЌ
ЁрBE2=BD2+DE2ЃЌ
ЁпЁЯBAC=ЁЯDAE=90ЁуЃЌAB=ACЃЌAD=AEЃЌ
ЁрDE2=2AD2ЃЌBC2=2AB2ЃЌ
ЁпBC2=BD2+CD2ЁйBD2ЃЌ
Ёр2AB2=BD2+CD2ЁйBD2ЃЌ
ЁрBE2Ёй2ЃЈAD2+AB2ЃЉЃЌЁрЂмДэЮѓЃЎ
ЙЪД№АИЮЊЂйЂкЂлЃЎ
ЃЈ2ЃЉЂйНтЃКaЁЂШчЭМ2жаЃЌЕБЕуEдкABЩЯЪБЃЌBE=ABЉAE=2ЃЎ

ЁпЁЯEAC=90ЁуЃЌ
ЁрCE=![]() ЃЌ
ЃЌ
ЭЌЃЈ1ЃЉПЩжЄЁїADBЁеЁїAECЃЎ
ЁрЁЯDBA=ЁЯECAЃЎ
ЁпЁЯPEB=ЁЯAECЃЌ
ЁрЁїPEBЁзЁїAECЃЎ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЁрPB=![]() ЃЎ
ЃЎ
bЁЂШчЭМжаЃЌЕБЕуEдкBAбгГЄЯпЩЯЪБЃЌBE=6ЃЎ

ЁпЁЯEAC=90ЁуЃЌ
ЁрCE=![]()
ЭЌЃЈ1ЃЉПЩжЄЁїADBЁеЁїAECЃЎ
ЁрЁЯDBA=ЁЯECAЃЎ
ЁпЁЯBEP=ЁЯCEAЃЌ
ЁрЁїPEBЁзЁїAECЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрPB=![]()
злЩЯЃЌPB=![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЂкНтЃКШчЭМжаЃЌвдAЮЊдВаФADЮЊАыОЖЛдВЃЌЕБCEдкЁбAЩЯЗНгыЁбAЯрЧаЪБЃЌPBЕФжЕзюДѓЃЎ

РэгЩЃКДЫЪБЁЯBCEзюДѓЃЌвђДЫPBзюДѓЃЌЃЈЁїPBCЪЧжБНЧШ§НЧаЮЃЌаББпBCЮЊЖЈжЕЃЌЁЯBCEзюДѓЃЌвђДЫPBзюДѓЃЉ
ЁпAEЁЭECЃЌ
ЁрEC=![]() ЃЌ
ЃЌ
гЩЃЈ1ЃЉПЩжЊЃЌЁїABDЁеЁїACEЃЌ
ЁрЁЯADB=ЁЯAEC=90ЁуЃЌBD=CE=2![]() ЃЌ
ЃЌ
ЁрЁЯADP=ЁЯDAE=ЁЯAEP=90ЁуЃЌ
ЁрЫФБпаЮAEPDЪЧОиаЮЃЌ
ЁрPD=AE=2ЃЌ
ЁрPB=BD+PD=2![]() +2ЃЎ
+2ЃЎ
злЩЯЫљЪіЃЌPBГЄЕФзюДѓжЕЪЧ2![]() +2ЃЎ
+2ЃЎ

 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ