ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΓœAOBΘΫ100ΓψΘ§ΓœCODΘΫ40ΓψΘ§OEΘ§OFΖ÷±πΤΫΖ÷ΓœAODΘ§ΓœBOD.
(1)»γΆΦ1Θ§Β±OAΘ§OC÷ΊΚœ ±Θ§«σΓœEOFΒΡΕ» ΐΘΜ
(2)»τΫΪΓœCODΒΡ¥”ΆΦ1ΒΡΈΜ÷Ο»ΤΒψOΥ≥ ±’κ–ΐΉΣΘ§–ΐΉΣΫ«ΓœAOCΘΫΠΝΘ§«“0ΓψΘΦΠΝΘΦ90Γψ.
ΔΌ»γΆΦ2Θ§ ‘≈–ΕœΓœBOF”κΓœCOE÷°Φδ¬ζΉψΒΡ ΐΝΩΙΊœΒ≤ΔΥΒΟςάμ”….
ΔΎ‘ΎΓœCOD–ΐΉΣΙΐ≥Χ÷–Θ§«κ÷±Ϋ”–¥≥ωΓœBOEΘ§ΓœCOFΘ§ΓœAOC÷°ΦδΒΡ ΐΝΩΙΊœΒ.
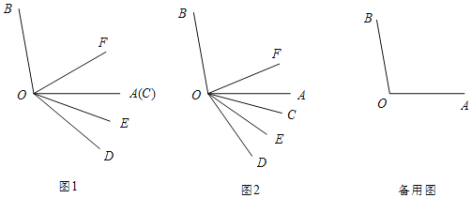
ΓΨ¥πΑΗΓΩ(1)ΓœEOF=50ΓψΘΜ(2)ΔΌΓœBOF+ΓœCOEΘΫ90ΓψΘΜάμ”…ΦϊΫβΈωΘΜΔΎΓœCOF+ΓœAOC©¹ΓœBOEΘΫ30Γψ.
ΓΨΫβΈωΓΩ
(1)”…Χβ“βΒΟ≥ωΓœAODΘΫΓœCODΘΫ40ΓψΘ§ΓœBODΘΫΓœAOB+ΓœCODΘΫ140ΓψΘ§”…Ϋ«ΤΫΖ÷œΏΕ®“εΒΟ≥ωΓœEODΘΫ![]() ΓœAODΘΫ20ΓψΘ§ΓœDOFΘΫ
ΓœAODΘΫ20ΓψΘ§ΓœDOFΘΫ![]() ΓœBODΘΫ70ΓψΘ§Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
ΓœBODΘΫ70ΓψΘ§Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
(2)ΔΌ”…Ϋ«ΤΫΖ÷œΏΕ®“εΒΟ≥ωΓœEODΘΫΓœAOEΘΫ![]() ΓœAODΘΫ20Γψ+
ΓœAODΘΫ20Γψ+![]() ΠΝΘ§ΓœBOFΘΫ
ΠΝΘ§ΓœBOFΘΫ![]() ΓœBODΘΫ70Γψ+
ΓœBODΘΫ70Γψ+![]() ΠΝΘ§«σ≥ωΓœCOEΘΫΓœAOE©¹ΓœAOCΘΫ20Γψ©¹
ΠΝΘ§«σ≥ωΓœCOEΘΫΓœAOE©¹ΓœAOCΘΫ20Γψ©¹![]() ΠΝΘ§Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
ΠΝΘ§Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
ΔΎ”…ΔΌΒΟΓœEODΘΫΓœAOEΘΫ20Γψ+![]() ΠΝΘ§ΓœDOFΘΫΓœBOFΘΫ70Γψ+
ΠΝΘ§ΓœDOFΘΫΓœBOFΘΫ70Γψ+![]() ΠΝΘ§
ΠΝΘ§
Β±ΓœAOCΘΦ40Γψ ±Θ§«σ≥ωΓœCOFΘΫΓœDOF©¹ΓœCODΘΫ30Γψ+![]() ΠΝΘ§ΓœBOEΘΫΓœBOD©¹ΓœEODΘΫΓœAOB+ΓœCOD+ΠΝ©¹ΓœEODΘΫ120Γψ+
ΠΝΘ§ΓœBOEΘΫΓœBOD©¹ΓœEODΘΫΓœAOB+ΓœCOD+ΠΝ©¹ΓœEODΘΫ120Γψ+![]() ΠΝΘ§Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
ΠΝΘ§Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
Β±40ΓψΘΦΓœAOCΘΦ90Γψ ±Θ§«σ≥ωΓœCOFΘΫΓœDOF+ΓœDOCΘΫ150Γψ©¹![]() ΠΝΘ§ΓœBOEΘΫΓœBOD©¹ΓœDOEΘΫ120Γψ+
ΠΝΘ§ΓœBOEΘΫΓœBOD©¹ΓœDOEΘΫ120Γψ+![]() Θ§Φ¥Ω…ΒΟ≥ω¥πΑΗ.
Θ§Φ¥Ω…ΒΟ≥ω¥πΑΗ.
ΫβΘΚ(1)ΓΏOAΘ§OC÷ΊΚœΘ§
ΓύΓœAODΘΫΓœCODΘΫ40ΓψΘ§ΓœBODΘΫΓœAOB+ΓœCODΘΫ100Γψ+40ΓψΘΫ140ΓψΘ§
ΓΏOEΤΫΖ÷ΓœAODΘ§OFΤΫΖ÷ΓœBODΘ§
ΓύΓœEODΘΫ![]() ΓœAODΘΫ
ΓœAODΘΫ![]() ΓΝ40ΓψΘΫ20ΓψΘ§ΓœDOFΘΫ
ΓΝ40ΓψΘΫ20ΓψΘ§ΓœDOFΘΫ![]() ΓœBODΘΫ
ΓœBODΘΫ![]() ΓΝ140ΓψΘΫ70ΓψΘ§
ΓΝ140ΓψΘΫ70ΓψΘ§
ΓύΓœEOFΘΫΓœDOF©¹ΓœEODΘΫ70Γψ©¹20ΓψΘΫ50ΓψΘΜ
(2)ΔΌΓœBOF+ΓœCOEΘΫ90ΓψΘΜάμ”…»γœ¬ΘΚ
ΓΏOEΤΫΖ÷ΓœAODΘ§OFΤΫΖ÷ΓœBODΘ§
ΓύΓœEODΘΫΓœAOEΘΫ![]() ΓœAODΘΫ
ΓœAODΘΫ![]() (40Γψ+ΠΝ)ΘΫ20Γψ+
(40Γψ+ΠΝ)ΘΫ20Γψ+![]() ΠΝΘ§ΓœBOFΘΫ
ΠΝΘ§ΓœBOFΘΫ![]() ΓœBODΘΫ
ΓœBODΘΫ![]() (ΓœAOB+ΓœCOD+ΠΝ)ΘΫ
(ΓœAOB+ΓœCOD+ΠΝ)ΘΫ![]() (100Γψ+40Γψ+ΠΝ)ΘΫ70Γψ+
(100Γψ+40Γψ+ΠΝ)ΘΫ70Γψ+![]() ΠΝΘ§
ΠΝΘ§
ΓύΓœCOEΘΫΓœAOE©¹ΓœAOCΘΫ20Γψ+![]() ΠΝ©¹ΠΝΘΫ20Γψ©¹
ΠΝ©¹ΠΝΘΫ20Γψ©¹![]() ΠΝΘ§
ΠΝΘ§
ΓύΓœBOF+ΓœCOEΘΫ70Γψ+![]() ΠΝ+20Γψ©¹
ΠΝ+20Γψ©¹![]() ΠΝΘΫ90ΓψΘΜ
ΠΝΘΫ90ΓψΘΜ
ΔΎ”…ΔΌΒΟΘΚΓœEODΘΫΓœAOEΘΫ20Γψ+![]() ΠΝΘ§ΓœDOFΘΫΓœBOFΘΫ70Γψ+
ΠΝΘ§ΓœDOFΘΫΓœBOFΘΫ70Γψ+![]() ΠΝΘ§
ΠΝΘ§
Β±ΓœAOCΘΦ40Γψ ±Θ§»γΆΦ2Υυ ΨΘΚ
ΓœCOFΘΫΓœDOF©¹ΓœCODΘΫ70Γψ+![]() ΠΝ©¹40ΓψΘΫ30Γψ+
ΠΝ©¹40ΓψΘΫ30Γψ+![]() ΠΝΘ§
ΠΝΘ§
ΓœBOEΘΫΓœBOD©¹ΓœEODΘΫΓœAOB+ΓœCOD+ΠΝ©¹ΓœEODΘΫ100Γψ+40Γψ+ΠΝ©¹(20Γψ+![]() ΠΝ)ΘΫ120Γψ+
ΠΝ)ΘΫ120Γψ+![]() ΠΝΘ§
ΠΝΘ§
ΓύΓœBOE+ΓœCOF©¹ΓœAOCΘΫ120Γψ+![]() ΠΝ+30Γψ+
ΠΝ+30Γψ+![]() ΠΝ©¹ΠΝΘΫ150ΓψΘ§
ΠΝ©¹ΠΝΘΫ150ΓψΘ§
Β±40ΓψΘΦΓœAOCΘΦ90Γψ ±Θ§»γΆΦ3Υυ ΨΘΚ
ΓœCOFΘΫΓœDOF+ΓœDOCΘΫ![]() (360Γψ©¹140Γψ©¹ΠΝ)+40ΓψΘΫ150Γψ©¹
(360Γψ©¹140Γψ©¹ΠΝ)+40ΓψΘΫ150Γψ©¹![]() ΠΝΘ§
ΠΝΘ§
ΓœBOEΘΫΓœBOD©¹ΓœDOEΘΫ140Γψ+ΠΝ©¹(20Γψ+![]() ΠΝ)ΘΫ120Γψ+
ΠΝ)ΘΫ120Γψ+![]() Θ§
Θ§
ΓύΓœCOF+ΓœAOC©¹ΓœBOEΘΫ150Γψ©¹![]() +ΠΝ©¹(120Γψ+
+ΠΝ©¹(120Γψ+![]() )ΘΫ30ΓψΘΜ
)ΘΫ30ΓψΘΜ
Ήέ…œΥυ ωΘ§ΓœBOEΘ§ΓœCOFΘ§ΓœAOC÷°ΦδΒΡ ΐΝΩΙΊœΒΈΣΓœBOE+ΓœCOF©¹ΓœAOCΘΫ150ΓψΜρΓœCOF+ΓœAOC©¹ΓœBOEΘΫ30Γψ.



ΓΨΧβΡΩΓΩΡ≥ΨΑΒψΒΡΟ≈Τ±ΦέΗώ»γ±μΘΚ
ΙΚΤ±»Υ ΐ/»Υ | 1ΓΪ50 | 51ΓΪ100 | 100“‘…œ |
ΟΩ»ΥΟ≈Τ±Φέ/‘Σ | 12 | 10 | 8 |
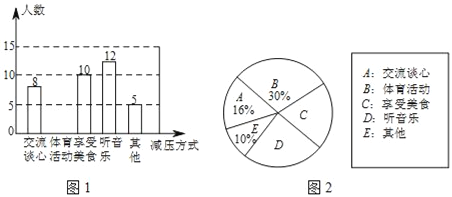
Ρ≥–ΘΤΏΡξΦΕΘ®1Θ©ΓΔΘ®2Θ©ΝΫΑύΦΤΜ°»Ξ”ΈάάΗΟΨΑΒψΘ§Τδ÷–Θ®1Θ©Αύ»Υ ΐ…Ό”Ύ50»ΥΘ§Θ®2Θ©Αύ»Υ ΐΕύ”Ύ50»Υ«“…Ό”Ύ100»ΥΘ§»γΙϊΝΫΑύΕΦ“‘ΑύΈΣΒΞΈΜΒΞΕάΙΚΤ±Θ§‘ρ“ΜΙ≤÷ßΗΕ1118‘ΣΘΜ»γΙϊΝΫΑύΝΣΚœΤπά¥ΉςΈΣ“ΜΗωΆ≈ΧεΙΚΤ±Θ§‘ρ÷Μ–ηΜ®Ζ―816‘ΣΘ°
Θ®1Θ©ΝΫΗωΑύΗς”–Εύ…ΌΟϊ―ß…ζΘΩ
Θ®2Θ©Ά≈ΧεΙΚΤ±”κΒΞΕάΙΚΤ±œύ±»ΫœΘ§ΝΫΗωΑύΗςΫΎ‘ΦΝΥΕύ…Ό«°ΘΩ