题目内容
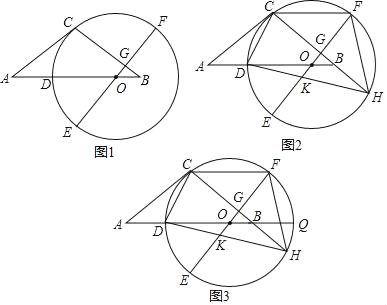
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆与AC相切于点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G.
(1)求证:D是弧EC的中点;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点K,连接CF,求证:CF=OK+DO;
(3)如图3,在(2)的条件下,延长DB交⊙O于点Q,连接QH,若DO=![]() ,KG=2,求QH.
,KG=2,求QH.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】(1)如图1中,连接OC,根据等角的余角相等,证明即可.
(2)如图2中,连接OC,首先证明,再证明点K在以F为圆心FC为半径的圆上即可解决问题;
(3)如图3中,连接OC、作HM⊥AQ于M.设OK=x,则CF= ![]() ,OG=2-x,GF=
,OG=2-x,GF=![]() ,根据CG2=CF2-FG2=CO2-OG2,列出方程求出x,再想办法求出HM、MQ即可解决问题.
,根据CG2=CF2-FG2=CO2-OG2,列出方程求出x,再想办法求出HM、MQ即可解决问题.
(1)证明:如图1中,连接OC.
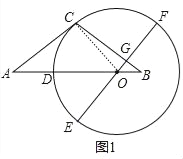
∵AC是⊙O的切线,
∴OC⊥AC,
∴∠ACO=90°,
∴∠A+∠AOC=90°,
∵CA=CB,
∴∠A=∠B,
∵EF⊥BC,
∴∠OGB=90°,
∴∠B+∠BOG=90°,
∴∠BOG=∠AOC,
∵∠BOG=∠DOE,
∴∠DOC=∠DOE,
∴点D是![]() 的中点.
的中点.
(2)证明:如图2中,连接OC.
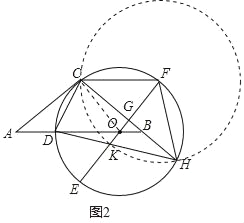
∵EF⊥HC,
∴CG=GH,
∴EF垂直平分HC,
∴FC=FH,
∵∠CFK=![]() ∠COE,
∠COE,
∵∠COD=∠DOE,
∴∠CFK=∠COD,
∵∠CHK=![]() ∠COD,
∠COD,
∴∠CHK=![]() ∠CFK,
∠CFK,
∴点K在以F为圆心FC为半径的圆上,
∴FC=FK=FH,
∵DO=OF,
∴DO+OK=OF+OK=FK=CF,
即CF=OK+DO;
(3)解:如图3中,连接OC、作HM⊥AQ于M.设OK=x,则CF=![]() +x,OG=2﹣x,GF=
+x,OG=2﹣x,GF=![]() ﹣(2﹣x),
﹣(2﹣x),

∵CG2=CF2﹣FG2=CO2﹣OG2,
∴(![]() +x)2﹣[
+x)2﹣[![]() (2﹣x)]2=(
(2﹣x)]2=(![]() )2﹣(2﹣x)2,
)2﹣(2﹣x)2,
解得x=![]() ,
,
∴CF=5,FG=4,CG=3,OG=![]() ,
,
∵∠CFE=∠BOG,
∴CF∥OB,
∴![]() =
=![]() =
=![]() ,
,
可得OB=![]() ,BG=
,BG=![]() ,BH=
,BH=![]() ,
,
由△BHM∽△BOG,可得![]() =
=![]() =
=![]() ,
,
∴BM=![]() ,HM=
,HM=![]() ,MQ=OQ﹣OB﹣BM=
,MQ=OQ﹣OB﹣BM=![]() ,
,
在Rt△HMQ中,QH=![]() =
=![]() =
=![]()
![]() .
.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案