题目内容
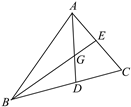
【题目】如图所示，△ABC的两条角平分线相交于一点G，∠BAC＝76°，∠ABE＝20°，求∠BEC，∠ADC的度数．
【答案】∠BEC＝96°；∠ADC＝78°.
【解析】
根据角平分线的性质得出∠EBC与∠ABC、∠DAC的度数，再根据三角形内角和定理求出∠C，即可得出结论.
∵BE平分∠ABC，∠ABE＝20°，
∴∠ABE＝∠EBC=
∠ABC＝20°，∠ABC＝40°，
又∵AD平分∠BAC，∠BAC＝76°，
∴∠DAC=∠BAC＝38°，
∠C=180°-∠ABC-∠BAC=180°-40°-76°=64°，
∴∠BEC=180°-∠EBC-∠C=180°-20°-64°=96°；
∠ADC=180°-∠DAC-∠C=180°-38°-64°=78°.
故答案为：∠BEC＝96°；∠ADC＝78°.
练习册系列答案
相关题目
