��Ŀ����
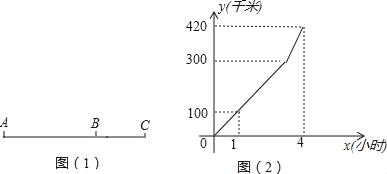
����Ŀ��ij��߳��ֱ��ż�����������ӹ�1000��ͬһ�ͺŵİ��˻Ἢ���ÿ������ÿ��ӹ�������ĸ�������ұ��ֲ��䣬����������Ҫ������һ�������Ƴ����쿪ʼ�ӹ����տ�ʼ�ӹ�ʱ���׳�����10�����ˣ��ҳ�����12�����ˣ�ͼ���߶�OB������ACB�ֱ��ʾ��������ļӹ����������ͼ���ṩ����Ϣ��������и��⣺
��1���߶�OB��ӳ������ ������ļӹ������
��2����ʼ�ӹ��׳���ӹ��������������ӹ�����������ͬ��
��3���������߶η�ӳ�ļӹ�������������һ�����⣬���������

���𰸡���1���ף���2���׳���ӹ�12���������ӹ��ļ���������ͬ����3���ҳ��������������ʱ��18�죬���ͬʱ�����������
��������
��1��ֱ��OB��б�ʽ�С����OB��ӳ���Ǽ׳���ӹ������
��2�����ݴ���ϵ��������ֱ��OB��OC�ĺ�������ʽ�������ʽ����������⣬�ɽ�������ӹ��ļ���������ͬʱ��ʱ�������
��3���ҳ�������������������ʱ�䣮
�⣺��1���߶�OB��ӳ���� �׳���ļӹ������
�ʴ�Ϊ���ף�
��2���������֪��ֱ��OB����ʽ��y=50x��A��2��0����C��18��960����
��ֱ��AC����ʽΪ��y=kx+b��
��![]() ��
��
��ã�k=60��b=��120,
ֱ��AC����ʽ��y=60x��120,
������![]() ��
��
��ã�![]() ��
��
�𣺼׳���ӹ�12���������ӹ��ļ���������ͬ��
��3�����⣺�ҳ����������ʱ��Ҫ�����죬���ͬʱ�����������
��BC�ĺ�������ʽΪ��y=kx+b��
��B��20��1000��C��18��960����
��![]() ��
��
��ã�![]() ,
,
��y=20x+600��
��y=1000ʱ���ã�x=20,
20��2=18���죩��
���ҳ��������������ʱ��18�죬���ͬʱ�����������

����Ŀ���±��dz���ij��Ů�������ؼ������
���أ�kg�� | 34 | 35 | 38 | 40 | 42 | 45 | 50 |
���� | 1 | 2 | 5 | 5 | 4 | 2 | 1 |
���ݱ�����Ϣ���ش��������⣺
��1���ð�Ů�����ص���λ������
��2���ð�Ů����ƽ��������kg��
��3�������ϱ��е����ݲ�ȫ����ͳ��ͼ�� 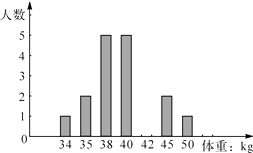
����Ŀ��ijѧУ��1500��ѧ���μ��조�Ұ����ǵĿ��á�Ϊ�����ͼƬ�������������������ȡ���ֲ���ѧ���ijɼ�����������������ͼ����ͼ��
������ | Ƶ�� | Ƶ�� |
60��x��70 | 40 | 0.40 |
70��x��80 | 35 | b |
80��x��90 | a | 0.15 |
90��x��100 | 10 | 0.10 |
Ƶ�ʷֲ�ͳ�Ʊ�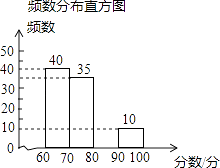
�����������Ϣ������������⣺
��1���ֱ����a��b��ֵ��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3������������ɼ�80�����ϣ���80�֣���Ϊ���㣬��ô�������Ƕ��٣����ҹ����У����ѧ����������������