题目内容
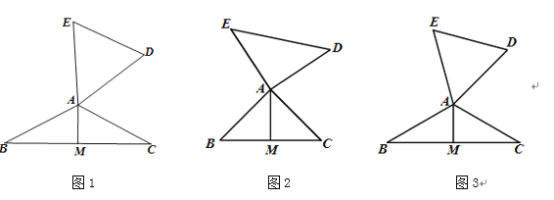
【题目】(1)如图(1),已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN.求出∠BQM的度数;
(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、…正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
正多边形 | 正方形 | 正五边形 | …… | 正n边形 |
∠BQM的度数 |
|
| …… |
|
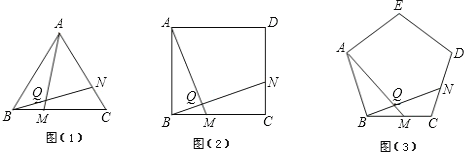
【答案】(1)∠BQM=∠60°;(2)90°;108°;![]() .
.
【解析】
(1)根据等边三角形的性质、SAS定理证明△ABM≌△BCN,根据三角形的外角的性质求出∠BQM;(2)仿照(1)的结论,计算即可.
(1)∵△ABC为等边三角形,
∴∠ABC=∠C=60°,AB=BC
在△ABM和△BCN中, 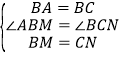 ,
,
∴△ABM≌△BCN,
∴∠BAM=∠CBN,
∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=60°;
(2) 90°;108°;![]() .
.

练习册系列答案
相关题目