Question

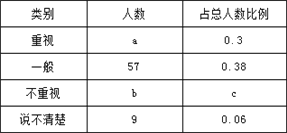
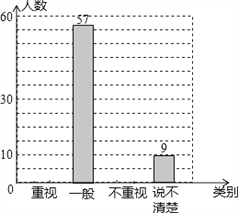
【题目】某加工厂为赶制一批零件，通过提高加工费标准的方式调动工人积极性.工人每天加工零件获得的加工费y（元）与加工个数x（个）之间的部分函数图象为折线OA-AB-BC，如图所示.

（1）求工人一天加工零件不超过20个时每个零件的加工费.

（2）求40≤≤60时y与x的函数关系式.

（3）小王两天一共加工了60个零件，共得到加工费220元.在这两天中，小王第一天加工零件不足20个，求小王第一天加工的零件个数.

Answer 1

【答案】（1）3元；（2） .（3）小王第一天加工10个零件

【解析】解：（1）由图象可知，当0≤x≤20时，每个零件的加工费为60÷20=3元，

即工人一天加工零件不超过20个时，每个零件的加工费为3元。

（2）当40≤x≤60时，设y与x的函数关系式为y=kx+b，

将B（40，140），C（60，240）代入，得

，解得。

∴y与x的函数关系式为y=5x－60。

（3）设小王第一天加工零件的个数为a，则第二天加工零件的个数为（60－a），

∵ 小王第一天加工的零件不足20个，小王两天一共加工了60个零件。

∴小王第二天加工的零件不足60个，超过40个。

由（2）知，第二天加工零件的加工费为5（60－a)－60。

∴5（60－a)－60=220－3a，解得，a =10。

∴小王第一天加工零件10个。

（1）当0≤x≤20时，由图象得出每个零件的加工费为60÷20=3元。

（2）当40≤x≤60时，设y与x的函数关系式为y=kx+b，将（20，60），（40，140）代入，列方程组求k、b的值即可。

（3）设小王第一天加工零件的个数为a，则第二天加工零件的个数为（60－a），由（2）知，第二天加工零件的加工费为5（60－a)－60，因此列方程5（60－a)－60=220－3a求解。