ƒøƒ⁄»ð
°æƒø°ø“—÷™πÿ”⁄xµƒ∑Ω≥Ãkx2+£®2k+1£©x+2=0£Æ
£®1£©«Û÷§£∫ŒÞ¬€k»°»Œ∫Œ µ ˝ ±£¨∑Ω≥Ã◊Д– µ ˝∏˘£ª
£®2£©µ±≈◊ŒÔœþy=kx2+£®2k+1£©x+2ÕºœÛ”Îx÷·¡Ω∏ˆΩªµ„µƒ∫·◊¯±Íæ˘Œ™’˚ ˝£¨«“kŒ™’˝’˚ ˝ ±£¨»ÙP£®a£¨y1£©£¨Q£®1£¨y2£© «¥À≈◊ŒÔœþ…œµƒ¡Ωµ„£¨«“y1£æy2£¨«ÎΩ·∫œ∫Ø ˝ÕºœÛ»∑∂® µ ˝aµƒ»°÷µ∑∂Œß£ª
£®3£©“—÷™≈◊ŒÔœþy=kx2+£®2k+1£©x+2∫„π˝∂®µ„£¨«Û≥ˆ∂®µ„◊¯±Í£Æ
°æ¥∞∏°ø£®1£©÷§√˜º˚Ω‚Œˆ£ª£®2£©a£æ1ªÚa£º©Å4£ª£®3£©≈◊ŒÔœþ∫„π˝∂®µ„£®0£¨2£©°¢£®©Å2£¨0£©£Æ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©∑÷¿ýÃ÷¬€£∫∏√∑Ω≥à «“ª‘™“ª¥Œ∑Ω≥Ã∫Õ“ª‘™∂˛¥Œ∑Ω≥áΩ÷÷«Èøˆ£Æµ±∏√∑Ω≥ÃŒ™“ª‘™∂˛¥Œ∑Ω≥à ±£¨∏˘µƒ≈–± Ω°˜°ð0£¨∑Ω≥Ã◊Д– µ ˝∏˘£ª
£®2£©Õ®π˝Ω‚kx2+£®2k+1£©x+2=0µ√µΩk=1£¨”…¥Àµ√µΩ∏√≈◊ŒÔœþΩ‚Œˆ ΩŒ™y=x2+3x+2£¨Ω·∫œÕºœÛªÿ¥Œ £Æ
£®3£©∏˘æð“‚µ√µΩkx2+£®2k+1£©x+2-y=0∫„≥…¡¢£¨”…¥À¡–≥ˆπÿ”⁄x°¢yµƒ∑Ω≥Ã◊È£¨Õ®π˝Ω‚∑Ω≥Ã◊È«Ûµ√∏√∂®µ„◊¯±Í£Æ
‘Ã‚Ω‚Œˆ£∫£®1£©÷§√˜£∫¢Ÿµ±k=0 ±£¨∑Ω≥ÃŒ™x+2=0£¨À˘“‘x=©Å2£¨∑Ω≥Ô– µ ˝∏˘£¨
¢⁄µ±k°Ÿ0 ±£¨°þ°˜=£®2k+1£©2©Å4k°¡2=£®2k©Å1£©2°ð0£¨º¥°˜°ð0£¨
°ýŒÞ¬€k»°»Œ∫Œ µ ˝ ±£¨∑Ω≥Ã◊Д– µ ˝∏˘£ª
£®2£©Ω‚£∫¡Óy=0£¨‘Úkx2+£®2k+1£©x+2=0£¨
Ω‚πÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥㨵√x1=©Å2£¨x2=©Å![]() £¨
£¨
°þ∂˛¥Œ∫Ø ˝µƒÕºœÛ”Îx÷·¡Ω∏ˆΩªµ„µƒ∫·◊¯±Íæ˘Œ™’˚ ˝£¨«“kŒ™’˝’˚ ˝£¨
°ýk=1£Æ
°ý∏√≈◊ŒÔœþΩ‚Œˆ ΩŒ™y=x2+3x+2£¨
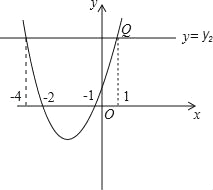
”…ÕºœÛµ√µΩ£∫µ±y1£æy2 ±£¨a£æ1ªÚa£º©Å4£Æ
£®3£©“¿Ã‚“‚µ√kx2+£®2k+1£©x+2©Åy=0∫„≥…¡¢£¨º¥k£®x2+2x£©+x©Åy+2=0∫„≥…¡¢£¨
‘Ú![]() £¨
£¨
Ω‚µ√![]() ªÚ
ªÚ![]() £Æ
£Æ
À˘“‘∏√≈◊ŒÔœþ∫„π˝∂®µ„£®0£¨2£©°¢£®©Å2£¨0£©£Æ

 ¡È–«º∆À„–°¥Ô»Àœµ¡–¥∞∏
¡È–«º∆À„–°¥Ô»Àœµ¡–¥∞∏ √œΩ®∆Ω¥Ì±朵¡–¥∞∏
√œΩ®∆Ω¥Ì±朵¡–¥∞∏°æƒø°øŒ™¡À∏¸∫√∏ƒ…∆∫”¡˜µƒÀÆ÷ £¨÷ŒŒ€π´Àææˆ∂®π∫¬Ú10ÀÆ¥¶¿Ì…˱∏![]() œ÷”–A£¨B¡Ω÷÷–Õ∫≈µƒ…˱∏£¨∆‰÷–√øº€∏Ò£¨‘¬¥¶¿ÌŒ€ÀÆ¡ø»Áœ¬±Ì£∫æ≠µ˜≤È£∫π∫¬Ú“ªÃ®A–Յ˱∏±»π∫¬Ú“ªÃ®B–Յ˱∏∂ý2ÕÚ‘™£¨π∫¬Ú2îA–Յ˱∏±»π∫¬Ú3îB–Յ˱∏…Ÿ6ÕÚ‘™£Æ
œ÷”–A£¨B¡Ω÷÷–Õ∫≈µƒ…˱∏£¨∆‰÷–√øº€∏Ò£¨‘¬¥¶¿ÌŒ€ÀÆ¡ø»Áœ¬±Ì£∫æ≠µ˜≤È£∫π∫¬Ú“ªÃ®A–Յ˱∏±»π∫¬Ú“ªÃ®B–Յ˱∏∂ý2ÕÚ‘™£¨π∫¬Ú2îA–Յ˱∏±»π∫¬Ú3îB–Յ˱∏…Ÿ6ÕÚ‘™£Æ
A–Õ | B–Õ | |
º€∏Ò | a | b |
¥¶¿ÌŒ€ÀÆ¡ø | 240 | 200 |
![]() «Ûa£¨bµƒ÷µ£ª
«Ûa£¨bµƒ÷µ£ª
![]() ÷ŒŒ€π´Àææ≠‘§À„π∫¬ÚŒ€ÀÆ¥¶¿Ì…˱∏µƒ◊ Ω≤ª≥¨π˝105ÕÚ‘™£¨ƒ„»œŒ™∏√π´Àæ”–ƒƒº∏÷÷π∫¬Ú∑Ω∞∏£ª
÷ŒŒ€π´Àææ≠‘§À„π∫¬ÚŒ€ÀÆ¥¶¿Ì…˱∏µƒ◊ Ω≤ª≥¨π˝105ÕÚ‘™£¨ƒ„»œŒ™∏√π´Àæ”–ƒƒº∏÷÷π∫¬Ú∑Ω∞∏£ª
![]() ‘⁄
‘⁄![]() µƒÃıº˛œ¬£¨»Ù√ø‘¬“™«Û¥¶¿ÌŒ€ÀÆ¡ø≤ªµÕ”⁄2040∂÷£¨Œ™¡ÀΩ⁄‘º◊ Ω£¨«Îƒ„Œ™÷ŒŒ€π´Àæ…˺∆“ª÷÷◊Ó °«Æµƒπ∫¬Ú∑Ω∞∏£Æ
µƒÃıº˛œ¬£¨»Ù√ø‘¬“™«Û¥¶¿ÌŒ€ÀÆ¡ø≤ªµÕ”⁄2040∂÷£¨Œ™¡ÀΩ⁄‘º◊ Ω£¨«Îƒ„Œ™÷ŒŒ€π´Àæ…˺∆“ª÷÷◊Ó °«Æµƒπ∫¬Ú∑Ω∞∏£Æ