Question

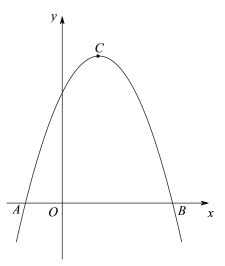
【题目】如图，在平面直角坐标系xOy中，点A1，A2，A3，…，An在y轴的正半轴上，点B1，B2，B3，…，Bn在二次函数y=x2位于第一象限的图象上，若△OB1A1，△A1B2A2，△A2B3A3，…，△An-1BnAn都是等腰直角三角形，其中∠B1=∠B2=∠B3=…=∠Bn=90°，则：点B1的坐标为______；线段A1A2的长为______；△An-1BnAn的面积为______．

Answer 1

【答案】（1，1）； 4； n2

【解析】

作B1C⊥y轴于C，B2D⊥y轴于D，如图，设OC=a，根据等腰直角三角形的性质得到OC=A1C=CB1=a，则B1（a，a），再把B1（a，a），代入y=x2得a1=0 (舍去)，a2=1，所以B1(1,1)，同理可得B2(2,4)，则线段A1A2长为4，利用上述规律得到An1An=2n，然后根据等腰直角三角形的面积公式计算△An-1BnAn的面积即可．

解：作B1C⊥y轴于C，B2D⊥y轴于D，如图，设OC=a，

∵△OB1A1为等腰直角三角形，

∴OC=A1C=CB1=a，

∴B1（a，a），

把B1（a，a）代入y=x2得a2=a，解得a1=0（舍去），a2=1，

∴B1（1，1），

设A1D=b，

∵△A1B2A2为等腰直角三角形，

∴A1D=A2D=DB2=b，

∴B2（b，b+2），

把B2（b，b+2）代入y=x2得b2=b+2，解得b1=-1（舍去），b2=2，

∴B2（2，4），

∴线段A1A2的长为4，

同理可得A2A3=6，An-1An=2n，

∴△An-1BnAn的面积=2nn=n2．

故答案为（1，1）；4；n2．