Question

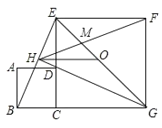
【题目】如图，在矩形ABCD（AD＞AB）中，P为BC边上的一点，AP＝AD，过点P作PE⊥PA交CD于E，连接AE并延长交BC的延长线于F．

（1）求证：△APE≌△ADE；

（2）若AB＝3，CP＝1，试求BP，CF的长；

（3）在（2）的条件下，连结PD，若点M为AP上的动点，N为AD延长线上的动点，且PM＝DN，连结MN交PD于G，作MH⊥PD，垂足为H，试问当M、N在移动过程中，线段GH的长度是否发生变化？若变化，请说明理由，若不变，求出GH的长．

Answer 1

【答案】（1）详见解析；（2）BP＝4，CF＝4；（3）没有变化，GH＝．

【解析】

（1）先判断出∠APE＝∠D＝90°，即可得出结论；

（2）先求出CD＝AB＝3，进而利用勾股定理求出CE＝，DE＝，再△ABP∽△PCE，即可得出BP＝4即可得出结论；

（3）先判断出MI＝DN，进而判断出△MGH≌△NGD，最后用勾股定理即可得出结论．

（1）证明：

∵在矩形ABCD中，∠D＝90°，又PE⊥PA，

∴∠APE＝∠D＝90°，

又∵AP＝AD，AE＝AE，

∴△APE≌△ADE

（2）由△APE≌△ADE得DE＝PE

∵AB＝3，

∴CD＝AB＝3

∴在Rt△PCE中，设CE＝x，则PE＝3﹣x，

∴（3﹣x）2＝x2+12，解得x＝

∴CE＝，DE＝

又∵∠B＝∠BCD＝∠APE＝90°

∴∠PEC+∠CPE＝90°，∠APB+∠CPE＝90°

∴∠PEC＝∠APB

∴△ABP∽△PCE

∴，得BP＝4

∴在Rt△ABP中，AP＝AD＝5，

又∵AD∥BC

∴ ，

∴CF＝4

（3）没有变化H

如图2，

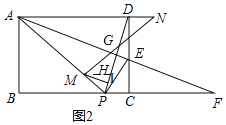
作MI∥DN交PD于I

∵AD＝AP，MI∥DN

∴∠ADP＝∠APD，∠ADP＝∠MIP

∴∠APD＝∠MIP

∴MI＝PM

又∵MH⊥PD

∴PH＝HI

又∵PM＝DN

∴MI＝DN

∴∠MGI＝∠DGN，∠IMG＝∠DNG，

∴△MGH≌△NGD

∴GI＝GD

∴GH＝GI+IH＝PD

∴在Rt△ABP中，，

∴GH＝．