题目内容
【题目】综合与实践:
问题情境:已知![]() 是正方形
是正方形![]() 的对角线,将直角三角尺放在正方形
的对角线,将直角三角尺放在正方形![]() 上.
上.
(1)如图1,使三角尺的直角顶点与点![]() 重合,三角尺的一条直角边交直线
重合,三角尺的一条直角边交直线![]() 于点
于点![]() ,另一条直角边交直线
,另一条直角边交直线![]() 于点
于点![]() .求证:
.求证:![]() .
.
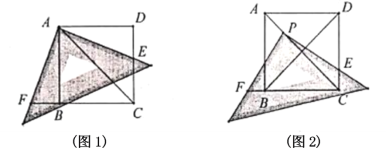
操作发现:
(2)如图2,将三角尺的直角项点![]() 放在
放在![]() 上,三角尺的一条直角边交直线
上,三角尺的一条直角边交直线![]() 于点
于点![]() ,另一条直角边交直线
,另一条直角边交直线![]() 于点
于点![]() .判断
.判断![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)证明见解析(2)![]() ;详见解析
;详见解析
【解析】
(1)根据同角的余角相等,证明∠DAE=∠BAF,再根据ASA证明ΔAFB≌ΔAED,根据全等三角形对应边相等即可得出结论;
(2)过点P作PM⊥BC于点M,作PN⊥DC于点N,由正方形的性质得到∠PMC=∠PNC=∠MCN=90°,∠ACB=∠ACD,再由角平分线的性质和四边形内角和为360°得到∠MPN=90°,PM=PN,然后根据同角的余角相等,证明∠MPF=∠NPE,再根据ASA证明ΔPFMΔPEN,根据全等三角形对应边相等即可得出结论.
(1)证明:∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
∵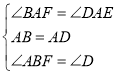
∴![]() (
(![]() )
)
∴![]() ;
;
(2)![]() .理由如下:
.理由如下:
过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,
,
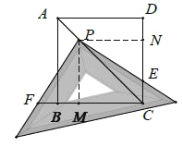
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,∠ABC=∠ACD,
,∠ABC=∠ACD,
∴![]() .
.
∵∠PMC+∠MCN+∠PNC+∠MPN=360°,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
∵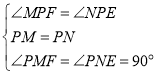 ,
,
∴![]() (
(![]() ),
),
∴![]() .
.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目