题目内容
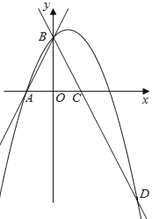
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,把
,把![]() 沿
沿![]() 轴对折,点
轴对折,点![]() 落到点
落到点![]() 处,过点
处,过点![]() 、
、![]() 的抛物线
的抛物线![]() 与直线
与直线![]() 交于点
交于点![]() 、
、![]() .
.
(1)求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在直线![]() 上方的抛物线上求一点
上方的抛物线上求一点![]() ,使
,使![]() 面积最大,求出点
面积最大,求出点![]() 坐标;
坐标;
(3)在第一象限内的抛物线上,是否存在一点![]() ,作
,作![]() 垂直于
垂直于![]() 轴,垂足为点
轴,垂足为点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为项点的三角形与
为项点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)由直线![]() 可以求出A,B的坐标,由待定系数法就可以求出抛物线的解析式和直线BD的解析式;
可以求出A,B的坐标,由待定系数法就可以求出抛物线的解析式和直线BD的解析式;
(2)先求得点D的坐标,作EF∥y轴交直线BD于F,设![]() ,利用三角形面积公式求得
,利用三角形面积公式求得![]() ,再利用二次函数性质即可求得答案;
,再利用二次函数性质即可求得答案;
(3)如图1,2,分类讨论,当△BOC∽△MON或△BOC∽△ONM时,由相似三角形的性质就可以求出结论;
(1)∵直线AB为![]() ,
,
令y=0,则![]() ,令
,令![]() ,则y=2,
,则y=2,
∴点A、B的坐标分别是:A (-1,0),B(0,2),
根据对折的性质:点C的坐标是:(1,0) ,
设直线BD解析式为![]() ,
,
把B(0,2),C(1,0)代入![]() ,得
,得![]() ,
,
解得:![]() ,
,![]() ,
,
∴直线BD解析式为![]() ,
,
把A(-1,0),B(0,2)代入![]() 得
得![]() ,
,
解得:![]() ,
,![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)解方程组![]() 得:
得: 和
和 ,
,
∴点D坐标为(3,-4) ,
作EF∥y轴交直线BD于F
设![]()
∴![]()
![]() (0<
(0<![]() <3)
<3)
∴当![]() 时,三角形面积最大,
时,三角形面积最大,
此时,点![]() 的坐标为:
的坐标为:![]() ;
;
(3)存在.
∵点B、C的坐标分别是B (0,2)、C (1,0),
∴![]() ,
,![]() ,
,
①如图1所示,
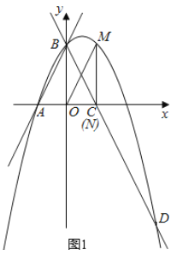
当△MON∽△BCO时,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
将![]() 代入抛物线的解析式
代入抛物线的解析式![]() 得:
得:
![]()
解得:![]() (不合题意,舍去),
(不合题意,舍去),![]() ,
,
∴点M的坐标为(1,2);
②如图2所示,
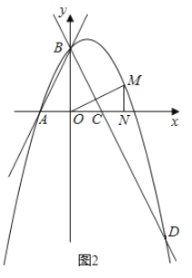
当△MON∽△CBO时,
∴![]() ,即
,即![]() ,
,
∴MN=![]() ON,
ON,
设![]() ,则M(b,
,则M(b,![]() b),
b),
将M(b,![]() b)代入抛物线的解析式
b)代入抛物线的解析式![]() 得:
得:
∴![]()
解得:![]() (不合题意,舍去),
(不合题意,舍去),![]() ,
,
∴点M的坐标为(![]() ,
,![]() ),
),
∴存在这样的点![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案