��Ŀ����
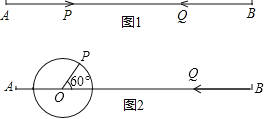
����Ŀ����֪���߶�AB��20cm.
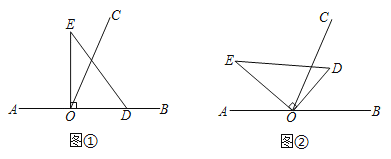
(1)��ͼ1����P���߶�AB��A����B����2����/���˶�����Q���߶�BA��B����A����3����/���˶�������________�룬��P��Q����������.
(2)��ͼ1����P���߶�AB��A����B����2����/���˶���ͬʱ��Q���߶�BA��B����A����3����/���˶������پ��������P��Q���5cm?
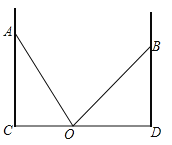
(3����ͼ2��AO��4cm��PO��2cm����POB��60������P���ŵ�O��60��/����ٶ���ʱ����תһ��ֹͣ��ͬʱ��Q��ֱ��BA��B����A���˶���������P��Q���������������Q�˶����ٶ�.
���𰸡���1��4����2��3���5�룻��3��9cm/s��2.8cm/s��
��������
��1���辭��x������������������·��Ϊ20cm���з�����⣻
��2���辭��a���P��Q���5cm���������������AB�ij�����P�͵�Q�ߵ�·�̣��õ�P�͵�Q�ߵ�·��AB�ij��ȣ��ֱ��з�����⣻
��3�����ڵ�P��Qֻ����ֱ��AB������������P��ת��ֱ��AB�ϵ�ʱ���������������Ը��������г����̷ֱ���⣮
�⣺��1���辭��x������������
��������2��3��x��20��
��ã�x��4��
������4�룬��P��Q����������
�ʴ�Ϊ��4��
��2���辭��a���P��Q���5cm��
������ã�20����2��3��a��5��
��ã�![]() ��
��
��2��3��a20��5��
��ã�a��5��
���پ���3���5���P��Q���5cm��
��3����P��Qֻ����ֱ��AB�����������P��ת��ֱ��AB�ϵ�ʱ��Ϊ![]() s��
s��![]() s��
s��
���Q���ٶ�Ϊycm/s��
��2sʱ������������ã�2y��202��18�����y��9
��5sʱ������������ã�5y��206��14�����y��2.8
�𣺵�Q���ٶ�Ϊ9cm/s��2.8cm/s��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�