题目内容
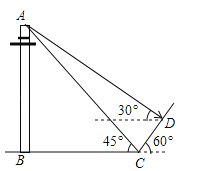
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
【答案】11m.
【解析】
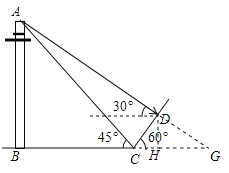
试题分析:延长AD交BC的延长线于G,作DH⊥BG于H,由三角函数求出求出CH、DH的长,得出CG,设AB=xm,根据正切的定义求出BG,得出方程,解方程即可.
试题解析:延长AD交BC的延长线于G,作DH⊥BG于H,如图所示:
在Rt△DHC中,∠DCH=60°,CD=4,则CH=CDcos∠DCH=4×cos60°=2,DH=CDsin∠DCH=4×sin60°=![]() ,∵DH⊥BG,∠G=30°,∴HG=
,∵DH⊥BG,∠G=30°,∴HG=![]() =
=![]() =6,∴CG=CH+HG=2+6=8,设AB=xm,∵AB⊥BG,∠G=30°,∠BCA=45°,∴BC=x,BG=
=6,∴CG=CH+HG=2+6=8,设AB=xm,∵AB⊥BG,∠G=30°,∠BCA=45°,∴BC=x,BG=![]() =
=![]() =
=![]() x,∵BG﹣BC=CG,∴
x,∵BG﹣BC=CG,∴![]() x﹣x=8,解得:x≈11(m);
x﹣x=8,解得:x≈11(m);
答:电线杆的高为11m.

练习册系列答案
相关题目