题目内容
【题目】如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y= ![]() 的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18. 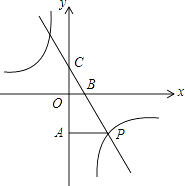
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
【答案】
(1)解:令一次函数y=kx+3中的x=0,则y=3,
即点C的坐标为(0,3),
∴AC=3﹣(﹣6)=9.
∵S△CAP= ![]() ACAP=18,
ACAP=18,
∴AP=4,
∵点A的坐标为(0,﹣6),
∴点P的坐标为(4,﹣6).
∵点P在一次函数y=kx+3的图象上,
∴﹣6=4k+3,解得:k=﹣ ![]() ;
;
∵点P在反比例函数y= ![]() 的图象上,
的图象上,
∴﹣6= ![]() ,解得:n=﹣24.
,解得:n=﹣24.
∴一次函数的表达式为y=﹣ ![]() x+3,反比例函数的表达式为y=﹣
x+3,反比例函数的表达式为y=﹣ ![]()
(2)解:令一次函数y=﹣ ![]() x+3中的y=0,则0=﹣
x+3中的y=0,则0=﹣ ![]() x+3,
x+3,
解得:x= ![]() ,
,
即点B的坐标为( ![]() ,0).
,0).
设点Q的坐标为(m,﹣ ![]()
![]() m+3).
m+3).
∵△OCQ的面积是△BCO面积的2倍,
∴|m|=2× ![]() ,解得:m=±
,解得:m=± ![]() ,
,
∴点Q的坐标为(﹣ ![]() ,9)或(
,9)或( ![]() ,﹣3)
,﹣3)
【解析】(1)由一次函数表达式可得出点C的坐标,结合A点坐标以及三角形的面积公式可得出AP的长度,从而得出点P的坐标,由点P的坐标结合待定系数法即可求出一次函数及反比例函数的表达式;(2)设点Q的坐标为(m,﹣ ![]() m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.
m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





