题目内容
【题目】如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
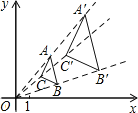
(1)请你根据位似的特征并结合点B的坐标变化回答下列问题:
①若点A(![]() ,3),则A′的坐标为______;
,3),则A′的坐标为______;
②△ABC与△A′B′C′的相似比为______;
(2)若△ABC的面积为m,求△A′B′C′的面积.(用含m的代数式表示)
【答案】(1)①(5,6),②1:2;(2)4m
【解析】
(1)①观察点B点和B′点的坐标得到位似比为2,然后根据此规律确定A′的坐标(5,6);
②利用对应点坐标的变化即可得出相似比;
(2)利用位似图形面积比等于相似比的平方进而得出答案.
解:(1)①∵△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,
∵点B(3,1),B′(6,2),∴位似比为2,
∴若点A(![]() ,3),则A′的坐标(5,6);
,3),则A′的坐标(5,6);
②△ABC与△A′B′C′的相似比为1:2;
故答案为(5,6),1:2;
(2)∵△ABC与△A'B'C'的相似比为1:2
∴![]() ,
,
而△ABC的面积为m,
∴△A′B′C′的面积=4m.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目