��Ŀ����
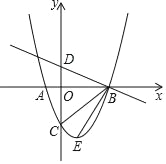
����Ŀ����ͼ������ֽ��ÿ��С�����DZ߳�Ϊ1�������Σ����ǰ��Ը�������Ϊ�ߵ������γ�Ϊ����������Ρ���ͼ�С�ABC���Ǹ�������Σ�������ͼ��ʾ��ƽ��ֱ������ϵ����C������Ϊ��0����1����
(1)����ͼ�ķ���ֽ�аѡ�ABC�Ե�OΪλ����������ʹ�Ŵ�ǰ���λ�Ʊ�Ϊ1��2��������A1B1C1����ABC���A1B1C1��λ������O������࣬A��B��C�Ķ�Ӧ��ֱ���A1��B1��C1����
(2)���ñ��ⷽ��ֽ�����A1B1C1���Բ��Բ��P�� P���������� ��.
(3)��(2)�е������£����P���ӻ�A1B1�ij���.
���𰸡�(1)ͼ��������(2) P��3��1������3��![]() .
.
��������
��1�����ù���ԭ��Ϊλ�����ĵ���ͼ�εĶ�Ӧ�������ϵд����A1��B2��C2�����꣬Ȼ����㼴�ɵõ���A1B2C2��
��2�����������ص㣬��A1C2��C2B2�Ĵ�ֱƽ���ߵõ���A1B2C2���Բ��Բ��P��Ȼ��д��P������ͼ���PA1��
��3�����������ص��֪��A1P A2=90�������û�����ʽ�������.
��1����ͼ��
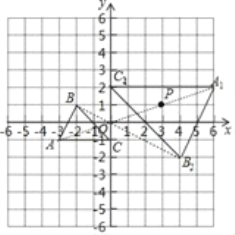
��2����P��������3��1����
��3��PA1=![]() =
=![]() ����A1P A2=90����
����A1P A2=90����
���ӻ�A1B1�ij���Ϊ![]() =
=![]()

��ϰ��ϵ�д�
 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
�����Ŀ