Question

【题目】已知等边△ABC内接于⊙O，AD为O的直径交线段BC于点M，DE∥BC，交AB的延长线于点E．

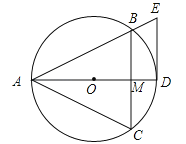
（1）求证：DE是⊙O的切线；

（2）若等边△ABC的边长为6，求BE的长．

Answer 1

【答案】（1）证明见解析（2）2

【解析】

试题分析：（1）由等边三角形的性质得出O即是△ABC的外心，又是△ABC的内心，得出∠BAM=∠CAM=30°，因此∠AMB=90°，由平行线的性质得出∠EDA=90°，即可得出结论；

（2）由等边三角形的性质得出BM=AB=3，连接OB，则∠OBM=30°，得出OM=OB，由勾股定理求出OB，由平行线的性质得出=，求出AE，即可得出BE的长．

（1）证明：∵等边△ABC内接于⊙O，

∴∠ABC=60°，O即是△ABC的外心，又是△ABC的内心，

∴∠BAM=∠CAM=30°，

∴∠AMB=90°，

∵DE∥BC，

∴∠EDA=∠AMB=90°，

∵AD为⊙O的直径，

∴DE是⊙O的切线；

（2）解：∵△ABC是等边三角形，

∴BM=AB=3，

连接OB，如图所示：

则∠OBM=30°，

∴OM=OB，

由勾股定理得：OB2﹣OM2=BM2，

即OB2﹣（OB）2=32，

解得：OB=2，

∴OM=，AM=3，AD=4，

∵DE∥BC，

∴=，即=，

解得：AE=8，

∴BE=AE﹣AB=8﹣6=2．