��Ŀ����
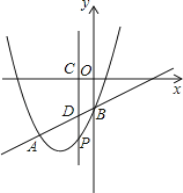
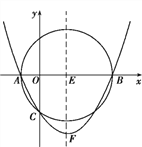
����Ŀ����ͼ����֪��E(3��0)ΪԲ�ģ�5Ϊ�뾶�Ĩ�E��x�ύ��A��B���㣬��y�ύ��C�㣬������y=ax2+bx+c(a��0)����A��B��C���㣬����ΪF.
(1)��A��B��C��������ꣻ
(2)�������ߵĽ���ʽ������F�����ꣻ
(3)��֪MΪ�������ϵ�һ����(����C���غ�)����̽����������A��B��MΪ������������������ABC�������ȣ������з��������ĵ�M�����ꣻ
����̽�����е�M��λ�ڵ������ޣ�����M���������߶���F�����ж�ֱ��MF�먑E��λ�ù�ϵ����˵������.
���𰸡���1��A(-2��0)��B(8��0)��C(0��-4)����2�������ߵĽ���ʽΪy=![]() x2-
x2-![]() x-4��F
x-4��F![]() ��(3)������M������Ϊ(6��-4)��(
��(3)������M������Ϊ(6��-4)��(![]() +3��4)��(-
+3��4)��(-![]() +3��4)������M��λ�ڵ������ޣ���M�㼴ΪM1�㣬��ʱֱ��MF�ͨ�E���У����ɼ�����.
+3��4)������M��λ�ڵ������ޣ���M�㼴ΪM1�㣬��ʱֱ��MF�ͨ�E���У����ɼ�����.
����������������1���������ֱ�ӵõ���A��B�����꣬����CE����Rt��OCE�У����ù��ɶ������OC�ij�����õ���C�����ꣻ
��2����֪��A��B��C�����꣬���ý���ʽ�����ϵ������������ߵĽ���ʽ���ɽ���ʽ�õ�����F�����ꣻ
��3���١�ABC�У��ױ�AB�ϵĸ�OC=4������ABC����ABM�����ȣ����������ϵĵ�M������������|yM|=4����˽ⷽ��yM=4��yM=-4������õ�M�����ꣻ
������ͼ���������ߣ������EM=5����˵�M�� E�ϣ������ù��ɶ������MF�ij��ȣ������ù��ɶ������涨�����ж���EMFΪֱ�������Σ���EMF=90��������ֱ��MF�� E���У�
�����(1)����ͼ�ɵõ�A�ĺ�����Ϊ3-5=-2����B�ĺ�����Ϊ3+5=8��
����CE����CE=5����OE=3��
��OC=![]() =4��
=4��
��A(-2��0)��B(8��0)��C(0��-4).
(2)��(-2��0)��(8��0)��(0��-4)����y=ax2+bx+c����.
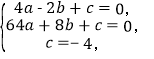 ���
���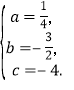
�������ߵĽ���ʽΪy=![]() x2-
x2-![]() x-4.
x-4.
��EF��y�ᣬ���F�ĺ�����Ϊ3.
��x=3����y=![]() x2-
x2-![]() x-4����y=-
x-4����y=-![]() ��
��
��F![]() .
.
(3)����ͼ��ʾ������AC��BM1��BC��
��֪![]() =S��ABC����ABM1����ABCͬ�ȸߣ�
=S��ABC����ABM1����ABCͬ�ȸߣ�
��C���M1����ֱ��x=3�Գƣ�
M1(6��-4).
��y=4����y=![]() x2-
x2-![]() x-4����
x-4����![]() x2-
x2-![]() x-4=4��
x-4=4��
���x1=![]() +3��x2=-
+3��x2=-![]() +3��
+3��
��M2(![]() +3��4)��M3(-
+3��4)��M3(-![]() +3��4).
+3��4).
�����з��������ĵ�M������Ϊ(6��-4)��(![]() +3��4)��(-
+3��4)��(-![]() +3��4).
+3��4).
����M��λ�ڵ������ޣ���M�㼴ΪM1�㣬��ʱֱ��MF�ͨ�E����.
�������£�M1(6��-4)��Բ��E(3��0)����F![]() ��
��
����M1E.
���ù��ɶ�����M1E=5��M1F=![]() ����EF=
����EF=![]() ��
��
��M1E2+M1F2=EF2������FM1E=90�㣬
��M1E��M1F.
��M1E�Ǩ�E�İ뾶��
��ֱ��M1F�ͨ�E���У�
����M��λ�ڵ�������ʱ��ֱ��MF�먑E����.

 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�����Ŀ��2014��ȫ���������������Ϊ��ό�����Ϸ��м���Ϊ���˽���ա������������⡱�ľ۽��㣬��������˺Ϸ��в��������Ե�����������������������ͼ��ʾ�IJ�������ͳ��ͼ����
��� | ���㻰�� | Ƶ���������� |
A | ʳƷ��ȫ | 80 |
B | ����ҽ�� | m |
C | ��ҵ���� | n |
D | ��̬���� | 120 |
E | ���� | 60 |
�����ͼ�����ṩ����Ϣ����������⣺
��1����գ�m= ��n= ������ͳ��ͼ��E����ռ�İٷֱ�Ϊ %��
��2���Ϸ����˿�����750���ˣ�����������й�עD�黰�������������
��3��������ν��ܵ���������У�������һ�ˣ�����˹�עC�黰��ĸ����Ƕ��٣�

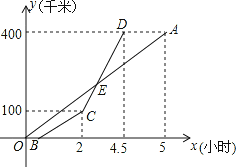
����Ŀ�����ִ�Ϊ�˶�һ�ι�·�����̻����ƻ�����![]() ��
��![]() ���ַ羰����900�ã�
���ַ羰����900�ã�![]() ��
��![]() �������������Ϣ���±���
�������������Ϣ���±���
Ʒ�� ��Ŀ | ���ۣ�Ԫ | �ɻ��� |
| 80 |
|
| 100 |
|
������![]() ����
����![]() �ã�����������ܷ���Ϊ
�ã�����������ܷ���Ϊ![]() Ԫ��
Ԫ��
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2�����������ܷ��ò�����82 000Ԫ����![]() ���������ڶ��ٿã�
���������ڶ��ٿã�
��3����ϣ���������ijɻ��ʲ�����![]() ����ʹ�������ܷ�����ͣ�Ӧѡ��
����ʹ�������ܷ�����ͣ�Ӧѡ��![]() ��
��![]() �����������ٿã���ʱ��ͷ���Ϊ���٣�
�����������ٿã���ʱ��ͷ���Ϊ���٣�