Question

【题目】如图，在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是_____．

Answer 1

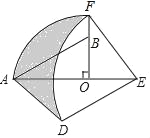
【答案】8﹣π

【解析】分析：

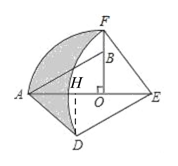
如下图，过点D作DH⊥AE于点H，由此可得∠DHE=∠AOB=90°，由旋转的性质易得DE=EF=AB，OE=BO=2，OF=AO=3，∠DEF=∠FEO+∠DEH=90°，∠ABO=∠FEO，结合∠ABO+∠BAO=90°可得∠BAO=∠DEH，从而可证得△DEH≌△BAO，即可得到DH=BO=2，再由勾股定理求得AB的长，即可由S阴影=S扇形AOF+S△OEF+S△ADE-S扇形DEF即可求得阴影部分的面积.

详解：

如下图，过点D作DH⊥AE于点H，

∴∠DHE=∠AOB=90°，

∵OA=3，OB=2，

∴AB=，

由旋转的性质结合已知条件易得：DE=EF=AB= ，OE=BO=2，OF=AO=3，∠DEF=∠FEO+∠DEH=90°，∠ABO=∠FEO，

又∵∠ABO+∠BAO=90°，

∴∠BAO=∠DEH，

∴△DEH≌△BAO，

∴DH=BO=2，

∴S阴影=S扇形AOF+S△OEF+S△ADE-S扇形DEF

=

=.

故答案为：.