题目内容
【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,连接CE、DF,将△CBE沿CE对折,得到△CGE,延长EG交CD的延长线于点H。

(1)求证:CE⊥DF;
(2)求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)运用△BCE≌Rt△CDF(SAS),再利用角的关系求得∠CKD=90°即可解题.
(2)设正方形ABCD的边长为2a,设CH=x,利用勾股定理求出a与x之间的关系即可解决问题.
(1)证明:设EC交DF于K.
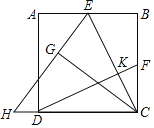
∵E,F分别是正方形ABCD边AB,BC的中点,
∴CF=BE,
在Rt△BCE和Rt△CDF中,
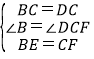 ,
,
∴△BCE≌Rt△CDF(SAS),
∠BCE=∠CDF,
又∵∠BCE+∠ECD=90°,
∴∠CDF+∠ECD=90°,
∴∠CKD=90°,
∴CE⊥DF.
(2)解:设正方形ABCD的边长为2a.
EB=EG,∠BEC=∠CEG,∠EGC=∠B=90°
∵CD∥AB,
∴∠ECH=∠BEC,∴∠ECH=∠CEH,
∴EH=CH,
∵BE=EG=a,CD=CG=2a,
在Rt△CGH中,设CH=x,
∴x2=(x-a)2+(2a)2,
∴x=![]() a,
a,
∴GH=EH-EG=![]() a-a=
a-a=![]() a,
a,
∴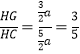 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目