题目内容
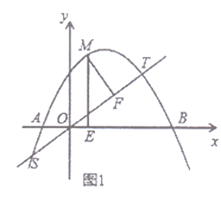
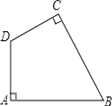
【题目】如图，在△ABC中，∠C＝90°，AB＝10，
，经过点C且与边AB相切的动圆与CA、CB分别交于点D、E，则线段DE长度的最小值是_____．
【答案】4.8
【解析】
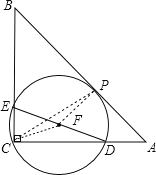
设DE的中点为F，圆F与AB的切点为P，连接FP，连接CF，CP，则有FP⊥AB；FC+FP＝DE，由三角形的三边关系知，CF+FP＞CP；只有当点F在CP上时，FC+FP＝PC有最小值为CP的长，即当点F在直角三角形ABC的斜边AB的高CP上时，DE＝CP有最小值，由直角三角形的面积公式知，此时CP＝BCAC÷AB＝4.8．
解：如图，设DE的中点为F，圆F与AB的切点为P，连接FP，连接CF，CP，则FP⊥AB．
∵AB＝10，
，
∴AC＝8，BC＝6
∵∠ACB＝90°，
∴FC+FP＝DE，
∴CF+FP＞CP，
∵当点F在直角三角形ABC的斜边AB的高CP上时，PC＝DE有最小值，
∴DE＝CP＝
＝4.8
故答案为4.8．
练习册系列答案
相关题目
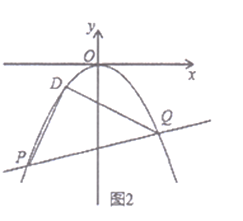
【题目】请你用学习“一次函数”时积累的经验和方法研究函数
的图象和性质，并解决问题．
完成下列步骤，画出函数的图象；
列表、填空；
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
描点：
连线
观察图象，当x______时，y随x的增大而增大；
结合图象，不等式
的解集为______．
