题目内容
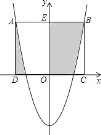
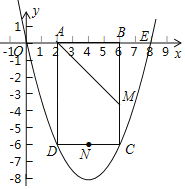
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于A(﹣2,0),点B(4,0).

(1)求抛物线的解析式;
(2)若点M是抛物线上的一动点,且在直线BC的上方,当S△MBC取得最大值时,求点M的坐标;
(3)在直线的上方,抛物线是否存在点M,使四边形ABMC的面积为15?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+x+4;(2)(2,4);(3)存在,(1,
x2+x+4;(2)(2,4);(3)存在,(1,![]() )或(3,
)或(3,![]() )
)
【解析】
(1)抛物线的表达式为::y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),故-8a=4,即可求解;
(2)根据题意列出S△MBC=![]() MH×OB=2(﹣
MH×OB=2(﹣![]() x2+x+4+x﹣4)=﹣x2+4x,即可求解;
x2+x+4+x﹣4)=﹣x2+4x,即可求解;
(3)四边形ABMC的面积S=S△ABC+S△BCM=![]() 6×4+(﹣x2+4x)=15,,即可求解.
6×4+(﹣x2+4x)=15,,即可求解.
解:(1)抛物线的表达式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),
故﹣8a=4,解得:a=﹣![]() ,
,
故抛物线的表达式为:y=﹣![]() x2+x+4;
x2+x+4;
(2)过点M作MH∥y轴交BC于点H,

将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣x+4,
设点M(x,﹣![]() x2+x+4),则点H(x,﹣x+4),
x2+x+4),则点H(x,﹣x+4),
S△MBC=![]() MH×OB=2(﹣
MH×OB=2(﹣![]() x2+x+4+x﹣4)=﹣x2+4x,
x2+x+4+x﹣4)=﹣x2+4x,
∵﹣1<0,故S有最大值,此时点M(2,4);
(3)四边形ABMC的面积S=S△ABC+S△BCM=![]() ×6×4+(﹣x2+4x)=15,
×6×4+(﹣x2+4x)=15,
解得:x=1或3,故点M(1,![]() )或(3,
)或(3,![]() ).
).

练习册系列答案
相关题目