题目内容
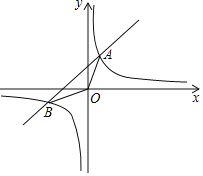
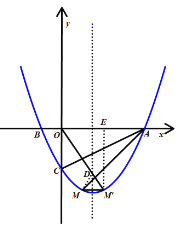
【题目】如图,点![]() 在抛物线
在抛物线![]() 上,且该抛物线与
上,且该抛物线与![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
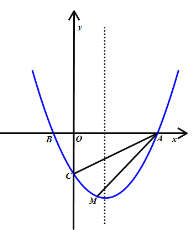
(1)求抛物线的解析式及对称轴;
(2)若点![]() 是抛物线对称轴上的一个动点,求
是抛物线对称轴上的一个动点,求![]() 的最小值;
的最小值;
(3)点![]() 是是抛物线上除点
是是抛物线上除点![]() 外的一点,若
外的一点,若![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)满足条件的点
;(3)满足条件的点![]() 有三个,分别是:
有三个,分别是:![]() ,
, ,
,
【解析】
(1)由已知M(1,-3)和B(-1,0),使用待定系数法解答即可;
(2)作点M(1,-3)关于对称轴的对称点为M1(2,-3),连接OM,则OD+MD的最小值为OD+DM=OM;
(3)①过M做MN∥AC交抛物线与点N1,直线MNi的解析式为为![]() ,与抛物线解析式联立求N;②过点M作MG⊥x轴,交AC于点H,过点G作N2N3∥AC,交抛物线与点N2,N3,则直线N2N3的解析式为
,与抛物线解析式联立求N;②过点M作MG⊥x轴,交AC于点H,过点G作N2N3∥AC,交抛物线与点N2,N3,则直线N2N3的解析式为![]() ,与抛物线解析式联立求N的坐标.
,与抛物线解析式联立求N的坐标.
(1)解:把点![]() 和
和![]() 代入抛物线
代入抛物线![]() ,得
,得![]()
解得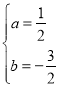
∴抛物线的解析式为:![]()
对称轴:![]()
(2)点![]() 关于对称轴对称的对称点
关于对称轴对称的对称点![]()
过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]()
![]() ,有最小值
,有最小值
∴![]()
(3)由(1)易知![]() ,
,![]()
∴得到直线![]() 解析式为
解析式为![]()
∵![]() ,
,
①过![]() 作
作![]() ,交抛物线于点
,交抛物线于点![]() ,
,
∵![]() ∴直线
∴直线![]() 解析式为
解析式为![]()
得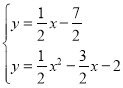
解得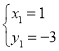 ,
,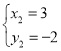
∴![]()
②过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 于点
于点![]() ,
,
![]() ,∴
,∴![]() ,
,![]()
过点![]() 作
作![]() ,,交抛物线于点
,,交抛物线于点![]() ,
,![]()
则直线![]() 解析式为
解析式为![]() ,
,
得:
解得: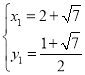 或
或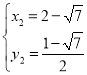
∴ ,
,
∴满足条件的点![]() 有三个,分别是:
有三个,分别是:![]() ,
, ,
,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目