题目内容
16、在正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.如果∠MAN在如图1所示的位置时,有BM+DN=MN成立(不必证明).请问当∠MAN绕点A旋转到如图2所示的位置时,线段BM、DN和MN之间又有怎样的数量关系?请说明理由.
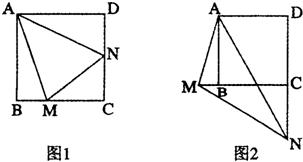

分析:在DN上截取DE=BM,连接AE,然后通过两步全等来求解;首先证△ADE≌△ABM,可得BM=DE,第二步,证△AMN≌△AEN,得到MN=NE,由此求得BM、DN、MN的数量关系.
解答: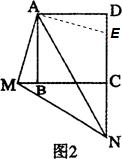 解:MN=DN-BM.
解:MN=DN-BM.
理由如下:
在DN上截取DE=BM,连接AE;
∵四边形ABCD是正方形,
∴∠ABM=∠D=90°,AB=AD,
又∵DE=BM,
∴△ABM≌△ADE,
∴AM=AE,∠BAM=∠DAE;
∵∠MAN=45°,∴∠DAE+∠BAN=∠MAB+∠BAN=45°,
∴∠EAN=∠MAN=45°,
又∵AM=AE,AN=AN,
∴△AMN≌△AEN,得MN=EN,
∴DN=DE+EN=BM+MN,即MN=DN-BM.
 解:MN=DN-BM.
解:MN=DN-BM.理由如下:
在DN上截取DE=BM,连接AE;
∵四边形ABCD是正方形,
∴∠ABM=∠D=90°,AB=AD,
又∵DE=BM,
∴△ABM≌△ADE,
∴AM=AE,∠BAM=∠DAE;
∵∠MAN=45°,∴∠DAE+∠BAN=∠MAB+∠BAN=45°,
∴∠EAN=∠MAN=45°,
又∵AM=AE,AN=AN,
∴△AMN≌△AEN,得MN=EN,
∴DN=DE+EN=BM+MN,即MN=DN-BM.
点评:此题主要考查了正方形的性质以及全等三角形的判定和性质,难度较大.

练习册系列答案
相关题目
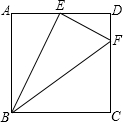 已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF=
已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF=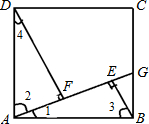 18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.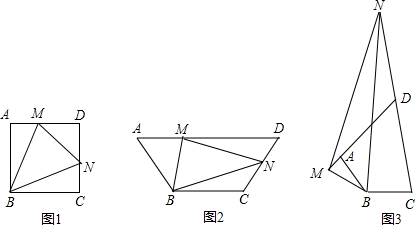
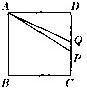 如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.
如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.