Question

如图，在正方形ABCD中，P是CD上一点，且AP=BC+CP，Q为CD中点，求证：∠BAP=2∠QAD．

Answer 1

分析：作∠BAC的平分线交BC于N，交DC的延长线于F，则CF=BC，进而求证△ABN≌△FCN，进而可得△ABN≌△ADQ，即∠BAN=∠DAQ，进而证明∠BAP=2∠QAD．

解答：解：作∠BAC的平分线交BC于N，交DC的延长线于F，CF=BC，

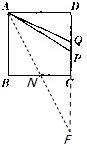
∵AB∥DF，∴∠BAN=∠CFN，
又∵CF=AB，∠FCN=∠ABN，
∴△ABN≌△FCN，
又∵AB=AD，∠ABN=∠ADQ，BN=DQ
∴△ABN≌△ADQ，
∠BAN=∠DAQ，
∴∠BAP=2∠QAD．

点评：本题考查了正方形各边长相等的性质，全等三角形的判定，全等三角形对应边、对应角相等的性质，本题中求证△ABN≌△ADQ是解题的关键．