题目内容
【题目】在等边△ABC中,点D为AC上一点,连接BD,直线l与AB,BD,BC分别相交于点E,P,F,且∠BPF=60°.
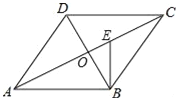
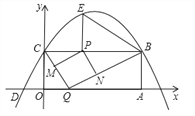
(1)如图(1),写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
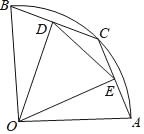
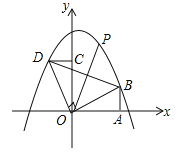
(2)若直线l向右平移到图(2),图(3)的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不需证明),若不成立,请说明理由;
(3)探究:如图(1),当BD满足什么条件时(其它条件不变),EF=![]() BF?请写出探究结果,并说明理由.
BF?请写出探究结果,并说明理由.

【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)先判断出∠BPF=∠EBF=60°,再结合公共角即可得出结论;
(2)同(2)的方法即可得出结论;
(3)由BD平分∠ABC得到∠ABP=∠PBF=30°,再由∠BPF=60°得到∠BEP=90°,从而得到∠BEF=30°,再利用锐角三角函数tan60°=![]() 即可得出结论.
即可得出结论.
(1)△BPF∽△EBF,△BPF∽△BCD.
以△BPF∽△EBF为例,证明如下:
∵∠BPF=∠EBF=60°,∠BFP=∠BFE,
∴△BPF∽△EBF.
(2)△BPF∽△EBF,△BPF∽△BCD成立.
(3)当BD平分∠ABC时,EF=![]() BF.理由如下:
BF.理由如下:
∵BD平分∠ABC,
∴∠ABP=∠PBF=30°.
∵∠BPF=60°,
∴∠BEP=90°,
∴∠BEF=60°-30°=30°.
在Rt△BEF中,∠EBF=60°,
∴tan60°=![]() ,即EF=
,即EF=![]() BF.
BF.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目