Ő‚ńŅńŕ»›
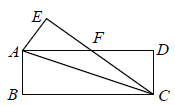
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨ĺō–őOABCĶńŃĹĪŖ‘ŕ◊ÝĪÍ÷Š…Ō£¨Ķ„AĶń◊ÝĪÍő™£®10£¨0£©£¨Ň◊őÔŌŖy=ax2+bx+4ĻżĶ„B£¨CŃĹĶ„£¨«“”Žx÷ŠĶń“ĽłŲĹĽĶ„ő™D£®©Ā2£¨0£©£¨Ķ„P «ŌŖ∂őCB…ŌĶń∂ĮĶ„£¨…ŤCP=t£®0£ľt£ľ10£©£ģ
£®1£©«Ž÷ĪĹ”–ī≥ŲB°ĘCŃĹĶ„Ķń◊ÝĪÍľįŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©ĻżĶ„P◊ųPE°ÕBC£¨ĹĽŇ◊őÔŌŖ”ŕĶ„E£¨Ń¨Ĺ”BE£¨ĶĪtő™ļő÷Ķ Ī£¨°ŌPBE=°ŌOCD£Ņ
£®3£©Ķ„Q «x÷Š…ŌĶń∂ĮĶ„£¨ĻżĶ„P◊ųPM°őBQ£¨ĹĽCQ”ŕĶ„M£¨◊ųPN°őCQ£¨ĹĽBQ”ŕĶ„N£¨ĶĪňńĪŖ–őPMQNő™’ż∑Ĺ–ő Ī£¨«Ž«ů≥ŲtĶń÷Ķ£ģ
°ĺīūįł°Ņ£®1£©B£®10£¨4£©£¨C£®0£¨4£©£¨![]() £Ľ£®2£©3£Ľ£®3£©
£Ľ£®2£©3£Ľ£®3£©![]() ĽÚ
ĽÚ ![]() .
.
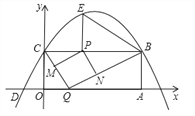
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©”…Ň◊őÔŌŖĶńĹ‚őŲ ĹŅ…«ůĶ√CĶ„◊ÝĪÍ£¨”…ĺō–őĶń–‘÷ Ņ…«ůĶ√BĶ„◊ÝĪÍ£¨”…B°ĘDĶń◊ÝĪÍ£¨ņŻ”√īż∂®ŌĶ ż∑®Ņ…«ůĶ√Ň◊őÔŌŖĹ‚őŲ Ĺ£Ľ
£®2£©Ņ……ŤP£®t£¨4£©£¨‘ÚŅ…ĪŪ ĺ≥ŲEĶ„◊ÝĪÍ£¨ī”∂ÝŅ…ĪŪ ĺ≥ŲPB°ĘPEĶń≥§£¨”…ŐűľĢŅ…÷§Ķ√°ųPBE°◊°ųOCD£¨ņŻ”√Ōŗň∆»żĹ«–őĶń–‘÷ Ņ…Ķ√ĶĹĻō”ŕtĶń∑Ĺ≥Ő£¨Ņ…«ůĶ√tĶń÷Ķ£Ľ
£®3£©ĶĪňńĪŖ–őPMQNő™’ż∑Ĺ–ő Ī£¨‘ÚŅ…÷§Ķ√°ųCOQ°◊°ųQAB£¨ņŻ”√Ōŗň∆»żĹ«–őĶń–‘÷ Ņ…«ůĶ√CQĶń≥§£¨‘ŕRt°ųBCQ÷–Ņ…«ůĶ√BQ°ĘCQ£¨‘ÚŅ…”√t∑÷ĪūĪŪ ĺ≥ŲPMļÕPN£¨Ņ…Ķ√ĶĹĻō”ŕtĶń∑Ĺ≥Ő£¨Ņ…«ůĶ√tĶń÷Ķ£ģ
‘Ő‚Ĺ‚őŲ£ļ
Ĺ‚£ļ£®1£©‘ŕy£Ĺax2£ębx£ę4÷–£¨ŃÓx£Ĺ0Ņ…Ķ√y£Ĺ4£¨
°ŗC£®0£¨4£©£¨
°ŖňńĪŖ–őOABCő™ĺō–ő£¨«“A£®10£¨0£©£¨
°ŗB£®10£¨4£©£¨
į—B°ĘD◊ÝĪÍīķ»ŽŇ◊őÔŌŖĹ‚őŲ ĹŅ…Ķ√![]() £¨
£¨
Ĺ‚Ķ√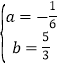 £¨
£¨
°ŗŇ◊őÔŌŖĹ‚őŲ Ĺő™y£Ĺ![]() x2£ę
x2£ę![]() x£ę4£Ľ
x£ę4£Ľ
£®2£©”…Ő‚“‚Ņ……ŤP£®t£¨4£©£¨‘ÚE£®t£¨![]() t2£ę
t2£ę![]() t£ę4£©£¨
t£ę4£©£¨
°ŗPB£Ĺ10©Āt£¨PE£Ĺ![]() t2£ę
t2£ę![]() t£ę4©Ā4£Ĺ
t£ę4©Ā4£Ĺ![]() t2£ę
t2£ę![]() t£¨
t£¨
°Ŗ°ŌBPE£Ĺ°ŌCOD£Ĺ90°„£¨
ĶĪ°ŌPBE£Ĺ°ŌOCD Ī£¨
‘Ú°ųPBE°◊°ųOCD£¨
°ŗ![]() £¨ľīBPOD£ĹCOPE£¨
£¨ľīBPOD£ĹCOPE£¨
°ŗ2£®10©Āt£©£Ĺ4£®![]() t2£ę
t2£ę![]() t£©£¨Ĺ‚Ķ√t£Ĺ3ĽÚt£Ĺ10£®≤ĽļŌŐ‚“‚£¨…Š»•£©£¨
t£©£¨Ĺ‚Ķ√t£Ĺ3ĽÚt£Ĺ10£®≤ĽļŌŐ‚“‚£¨…Š»•£©£¨
°ŗĶĪt£Ĺ3 Ī£¨°ŌPBE£Ĺ°ŌOCD£Ľ
ĶĪ°ŌPBE£Ĺ°ŌCDO Ī£¨
‘Ú°ųPBE/span>°◊°ųODC£¨
°ŗ![]() £¨ľīBPOC£ĹDOPE£¨
£¨ľīBPOC£ĹDOPE£¨
°ŗ4£®10©Āt£©£Ĺ2£®![]() t2£ę
t2£ę![]() t£©£¨Ĺ‚Ķ√t£Ĺ12ĽÚt£Ĺ10£®ĺý≤ĽļŌŐ‚“‚£¨…Š»•£©
t£©£¨Ĺ‚Ķ√t£Ĺ12ĽÚt£Ĺ10£®ĺý≤ĽļŌŐ‚“‚£¨…Š»•£©
◊Ř…Ōňý Ų°ŗĶĪt£Ĺ3 Ī£¨°ŌPBE£Ĺ°ŌOCD£Ľ
£®3£©ĶĪňńĪŖ–őPMQNő™’ż∑Ĺ–ő Ī£¨‘Ú°ŌPMC£Ĺ°ŌPNB£Ĺ°ŌCQB£Ĺ90°„£¨PM£ĹPN£¨
°ŗ°ŌCQO£ę°ŌAQB£Ĺ90°„£¨
°Ŗ°ŌCQO£ę°ŌOCQ£Ĺ90°„£¨
°ŗ°ŌOCQ£Ĺ°ŌAQB£¨
°ŗRt°ųCOQ°◊Rt°ųQAB£¨
°ŗ![]() £¨ľīOQAQ£ĹCOAB£¨
£¨ľīOQAQ£ĹCOAB£¨
…ŤOQ£Ĺm£¨‘ÚAQ£Ĺ10©Ām£¨
°ŗm£®10©Ām£©£Ĺ4°Ń4£¨Ĺ‚Ķ√m£Ĺ2ĽÚm£Ĺ8£¨
ĘŔĶĪm£Ĺ2 Ī£¨CQ£Ĺ![]() £Ĺ
£Ĺ![]() £¨BQ£Ĺ
£¨BQ£Ĺ![]() £Ĺ
£Ĺ![]() £¨
£¨
°ŗsin°ŌBCQ£Ĺ![]() £Ĺ
£Ĺ![]() £¨sin°ŌCBQ£Ĺ
£¨sin°ŌCBQ£Ĺ![]() £Ĺ
£Ĺ![]() £¨
£¨
°ŗPM£ĹPCsin°ŌPCQ£Ĺ![]() t£¨PN£ĹPBsin°ŌCBQ£Ĺ
t£¨PN£ĹPBsin°ŌCBQ£Ĺ![]() £®10©Āt£©£¨
£®10©Āt£©£¨
°ŗ![]() t £Ĺ
t £Ĺ![]() £®10©Āt£©£¨Ĺ‚Ķ√t£Ĺ
£®10©Āt£©£¨Ĺ‚Ķ√t£Ĺ![]() £¨
£¨
ĘŕĶĪm£Ĺ8 Ī£¨Õ¨ņŪŅ…«ůĶ√t£Ĺ![]() £¨
£¨
°ŗĶĪňńĪŖ–őPMQNő™’ż∑Ĺ–ő Ī£¨tĶń÷Ķő™![]() ĽÚ
ĽÚ![]() £ģ
£ģ

 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņő™ŃňŐŠłŖ—ß…ķ ť–īļļ◊÷Ķńń‹Ń¶£¨‘Ų«ŅĪ£Ľ§ļļ◊÷Ķń“‚ ∂£¨ő“ –ĺŔįžŃň ◊Ĺž°įļļ◊÷Őż–īīů»Ł°Ī£¨ĺ≠—°įőļů”–50√Ż—ß…ķ≤őľ”ĺŲ»Ł£¨’‚50√Ż—ß…ķÕ¨ ĪŐż–ī50łŲļļ◊÷£¨»Ű√Ņ’ż»∑Őż–ī≥Ų“ĽłŲļļ◊÷Ķ√1∑÷£¨łýĺ›≤‚ ‘≥…ľ®Ľś÷∆≥Ų≤Ņ∑÷∆Ķ ż∑÷≤ľĪŪļÕ≤Ņ∑÷∆Ķ ż∑÷≤ľ÷Ī∑ĹÕľ»ÁÕľĪŪ£ļ
◊ťĪū | ≥…ľ®x∑÷ | ∆Ķ ż£®»ň ż£© |
Ķŕ1◊ť | 25°‹x£ľ30 | 6 |
Ķŕ2◊ť | 30°‹x£ľ35 | 8 |
Ķŕ3◊ť | 35°‹x£ľ40 | 16 |
Ķŕ4◊ť | 40°‹x£ľ45 | a |
Ķŕ5◊ť | 45°‹x£ľ50 | 10 |

«ŽĹŠļŌÕľĪŪÕÍ≥…Ō¬Ń–łųŐ‚£ļ
£®1£©«ůĪŪ÷–aĶń÷Ķ£Ľ£®2£©«Žį—∆Ķ ż∑÷≤ľ÷Ī∑ĹÕľ≤Ļ≥šÕÍ’Ż£Ľ
£®3£©Ķŕ5◊ť10√ŻÕ¨—ß÷–£¨”–4√Żń–Õ¨—ߣ¨Ō÷Ĺę’‚10√ŻÕ¨—ß∆Ĺĺý∑÷≥…ŃĹ◊ťĹÝ––∂‘ŅĻŃ∑Ōį£¨«“4√Żń–Õ¨—ß√Ņ◊ť∑÷ŃĹ»ň£¨«ů–°”Ó”Ž–°«ŅŃĹ√Żń–Õ¨—ßń‹∑÷‘ŕÕ¨“Ľ◊ťĶńłŇ¬ £ģ
°ĺŐ‚ńŅ°Ņń≥…Ő≥°”ŻĻļĹÝĻŻ÷≠“ŻŃŌļÕŐľňŠ“ŻŃŌĻ≤60Ōš£¨ŃĹ÷÷“ŻŃŌ√ŅŌšĶńĹÝľŘļÕ ŘľŘ»ÁŌ¬ĪŪňý ĺ°£…ŤĻļĹÝĻŻ÷≠“ŻŃŌxŌš£®xő™’ż’Ż ż£©£¨«“ňýĻļĹÝĶńŃĹ÷÷“ŻŃŌń‹»ę≤Ņ¬Ű≥Ų£¨ĽŮĶ√Ķń◊‹ņŻ»ůő™W‘™£®◊Ę£ļ◊‹ņŻ»ů£Ĺ◊‹ ŘľŘ£≠◊‹ĹÝľŘ£©°£
£®1£©…Ť…Ő≥°ĻļĹÝŐľňŠ“ŻŃŌyŌš£¨÷ĪĹ”–ī≥Ųy”ŽxĶńļĮ żĹ‚őŲ Ĺ£Ľ
£®2£©«ů◊‹ņŻ»ůwĻō”ŕxĶńļĮ żĹ‚őŲ Ĺ£Ľ
£®3£©»ÁĻŻĻļĹÝŃĹ÷÷“ŻŃŌĶń◊‹∑—”√≤Ľ≥¨Ļż2100‘™£¨ń«√īł√…Ő≥°»ÁļőĹÝĽű≤Ňń‹ĽŮņŻ◊Ó∂ŗ£Ņ≤Ę«ů≥Ų◊ÓīůņŻ»ů°£
“ŻŃŌ | ĻŻ÷≠“ŻŃŌ | ŐľňŠ“ŻŃŌ |
ĹÝľŘ£®‘™/Ōš£© | 40 | 25 |
ŘľŘ£®‘™/Ōš£© | 52 | 32 |