题目内容
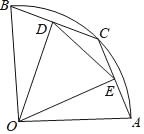
【题目】如图,在半径为1的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当![]() 时,求线段OD的长;
时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出是哪条边,并求其长度;如果不存在,请说明理由.
【答案】(1)OD=![]() ;(2)DE的长保持不变,理由见解析.
;(2)DE的长保持不变,理由见解析.
【解析】
(1)根据垂径定理得到BD=![]() BC=
BC=![]() ,根据勾股定理计算;
,根据勾股定理计算;
(2)连接AB,根据勾股定理求出AB,根据垂径定理,三角形中位线定理计算.
(1)∵OD⊥BC,
∴BD=![]() BC=
BC=![]() ,
,
∴OD=![]() =
=![]() ;
;
(2)DE的长保持不变,
理由如下:连接AB,
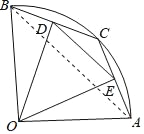
由勾股定理得,AB=![]() =
=![]() ,
,
∵OD⊥BC,OE⊥AC,
∴BD=CD,AE=EC,
∴DE=![]() AB=
AB=![]() .
.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目