题目内容
【题目】如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,∠OAB=30°.
(Ⅰ)若点C在y轴上,且△ABC为以AB为腰的等腰三角形,求∠BCA的度数;
(Ⅱ)若B(1,0),沿AB将△ABO翻折至△ABD.请根据题意补全图形,并求点D的横坐标.

【答案】(Ⅰ)30°或75°或15°;(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据等腰三角形的性质求角的度数,分点C在y轴的正负半轴两种情况求解即可;
(Ⅱ)通过题意补全图形后根据翻折和直角三角形30°角的性质即可求解.
解:(Ⅰ)如图:
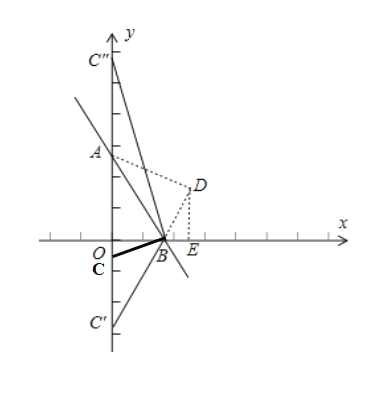
∵∠OAB=30°,当点C在y负半轴上时,△ABC为以AB为腰的等腰三角形,
如上图示,(1)当![]() 时,
时,
∴![]() ;
;
(2)当![]() 时,
时,
∴![]()
当点C在y轴正半轴上时,AB=AC″,
∴![]() ,
,
答:∠BCA的度数为30°或75°或15°.
(Ⅱ)如图:
沿AB将△ABO翻折至△ABD,过D点作DE⊥x轴于点E,
∵B(1,0),∴BD=OB=1,
∵∠OBA=∠DBA=60°,
∴∠DBE=60°,
∴∠BDE=30°,
∴BE=![]() DB=
DB=![]() ,
,
∴OE=OB+BE=![]() .
.
答:点D的横坐标为![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目