题目内容
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.

【答案】见解析
【解析】
(1)欲证明DF∥OA,只要证明OA⊥CD,DF⊥CD即可;
(2)过点作EM⊥OC于M,易知![]() ,只要求出EM、FM、FC即可解决问题;
,只要求出EM、FM、FC即可解决问题;
(1)证明:连接OD.
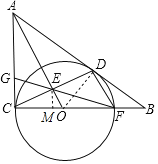
∵AB与⊙O相切与点D,又AC与⊙O相切与点,
∴AC=AD,∵OC=OD,
∴OA⊥CD,
∴CD⊥OA,
∵CF是直径,
∴∠CDF=90°,
∴DF⊥CD,
∴DF∥AO.
(2)过点作EM⊥OC于M,
∵AC=6,AB=10,
∴BC=![]() =8,
=8,
∴AD=AC=6,
∴BD=AB-AD=4,
∵BD2=BFBC,
∴BF=2,
∴CF=BC-BF=6.OC=![]() CF=3,
CF=3,
∴OA=![]() =3
=3![]() ,
,
∵OC2=OEOA,
∴OE=![]() ,
,
∵EM∥AC,
∴![]() ,
,
∴OM=![]() ,EM=
,EM=![]() ,FM=OF+OM=
,FM=OF+OM=![]() ,
,
∴![]() ,
,
∴CG=![]() EM=2.
EM=2.

练习册系列答案
相关题目