题目内容
【题目】已知BD、CE分别是△ABC的AC边、AB边上的高,M是BC边的中点,分别连结MD、ME、DE。

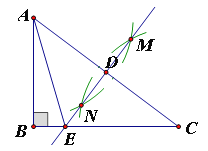
(1)当∠BAC<90°时,垂足D、E分别落在边AC、AB上,如图1,求证:DM=EM;
(2)若∠BAC=120°,试判断△DEM的形状,并说明理由;
(3)当∠BAC= 时,△DEM是等腰直角三角形。
【答案】(1)见解析;(2)△DEM是等边三角形,理由见解析;(3)当∠BAC=135°时,△DEM是等腰直角三角形.
【解析】
(1)DM是Rt△BCD斜边BC上的中线,EM是Rt△BCE斜边BC上的中线,根据直角三角形斜边上的中线的性质进行证明即可;
(2)根据等腰三角形的性质得到∠DBM=∠BDM,∠MEC=∠MCE,由三角形的外角的性质得到∠BME =2∠MCE,∠CMD =2∠DBM,根据三角形的内角和得到∠DBM+∠MCE=60°,即可得到结论;
(3)设∠BAC=x,同(2)可推出∠DME=2x180°,当∠DME=90°时求出x即可.
(1)证明:∵BD、CE是△ABC的两条高,M是BC的中点,
∴在Rt△BDC中,MD是斜边BC上的中线,
∴DM=![]() BC;
BC;
同理,得EM=![]() BC,
BC,
∴DM=EM;
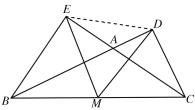
(2)如下图所示,∠BAC=120°,
∵BM=CM=DM=EM,
∴∠DBM=∠BDM,∠MEC=∠MCE,
∴∠BME=∠MEC+∠MCE=2∠MCE,∠CMD=∠DBM+∠BDM =2∠DBM,
∵∠BAC=120°,
∴∠DBM+∠MCE=60°,
∴∠BME+∠CMD=2(∠MCE +∠DBM)=120°,
∴∠DME=60°,
又∵DM=EM
∴△DEM是等边三角形;
(3)∵BM=CM=DM=EM,
∴∠DBM=∠BDM,∠MEC=∠MCE,
∴∠BME=2∠MCE,∠CMD=2∠DBM,
设∠BAC=x,
∴∠DBC+∠MCE=180°x,
∴∠BME+∠CMD=360°2x,
∴∠DME=180°(∠BME+∠CMD)=2x180°,
当∠DME=90°时,△DEM是等腰直角三角形,
所以2x180°=90°,解得x=135°,
故当∠BAC=135°时,△DEM是等腰直角三角形

 步步高达标卷系列答案
步步高达标卷系列答案