题目内容
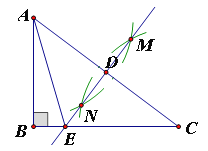
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 个单位
个单位![]() 的速度沿着线段
的速度沿着线段![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发也以
出发也以![]() 个单位
个单位![]() 的速度沿着线段
的速度沿着线段![]() 向终点
向终点![]() 运动,设运动时间为
运动,设运动时间为![]() .
.
![]() 填空:当
填空:当![]() 时,
时,![]() ________;
________;
![]() 当
当![]() 平分
平分![]() 时,直线
时,直线![]() 将菱形的周长分成两部分,求这两部分的比;
将菱形的周长分成两部分,求这两部分的比;
![]() 以
以![]() 为圆心,
为圆心,![]() 长为半径的
长为半径的![]() 是否能与直线
是否能与直线![]() 相切?如果能,求此时
相切?如果能,求此时![]() 的值;如果不能,说明理由.
的值;如果不能,说明理由.

【答案】![]() ;
;
【解析】
(1)过点P作PM⊥EF,垂足为M,利用锐角三角函数求得PM的长,然后利用勾股定理求得EM的长,再利用勾股定理求得PQ的长即可;
(2)根据题意画出图象,结合图形和已知条件证得△EPQ∽△FMQ,进而求得MC的长,然后求得菱形的周长被分成两部分,并据此求得两部分的比值;
(3)过P作PH⊥AD于H,并利用勾股定理PQ2=(![]() t)2+(4
t)2+(4![]() t)2后求得t的值即可.
t)2后求得t的值即可.
解:![]() 根据题意画出图形,如图所示:
根据题意画出图形,如图所示:
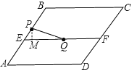
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
由题意可知![]() ,
,![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
即![]() ,则
,则![]() ,
,
根据勾股定理得:![]() ,
,
则![]() ,
,
在直角三角形![]() 中,根据勾股定理得:
中,根据勾股定理得:
![]() ;
;
![]() 根据题意画出图形,如图所示:
根据题意画出图形,如图所示:
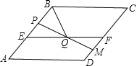
∵![]() 平分
平分![]()
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
设![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
则![]() ,
,![]() ,
,
则直线![]() 分菱形分成的两部分的周长分别为
分菱形分成的两部分的周长分别为![]() 和
和![]() ,
,
即菱形的周长被分为![]() 和
和![]() ,
,
所以这两部分的比为![]() ;
;![]() 过
过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() 点,
点,
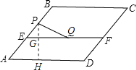
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
由题意可得方程![]() ,
,
解得:![]() .
.

练习册系列答案
相关题目