题目内容
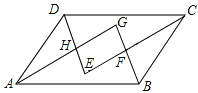
【题目】如图，在ABCD中，各内角的平分线分别相交于点E，F，G，H．
（1）求证：△ABG≌△CDE；
（2）猜一猜：四边形EFGH是什么样的特殊四边形？证明你的猜想；
（3）若AB=6，BC=4，∠DAB=60°，求四边形EFGH的面积．
【答案】（1）证明见解析；（2）矩形；（3）
．
【解析】试题分析：（1）根据角平分线的定义以及平行四边形的性质，即可得到AB=CD，∠BAG=∠DCE，∠ABG=∠CDE，进而判定△ABG≌△CDE；
（2）根据角平分线的定义以及平行四边形的性质，即可得出∠AGB=90°，∠DEC=90°，∠AHD=90°=∠EHG，进而判定四边形EFGH是矩形；
（3）根据含30°角的直角三角形的性质，得到BG，AG，BF，CF，进而得出EF和GF的长，可得四边形EFGH的面积．
试题解析：解：（1）∵GA平分∠BAD，EC平分∠BCD，∴∠BAG=
∠BAD，∠DCE=
∠DCB，∵ABCD中，∠BAD=∠DCB，AB=CD，∴∠BAG=∠DCE，同理可得，∠ABG=∠CDE，在△ABG和△CDE中，∵∠BAG=∠DCE，AB=CD，∠ABG=∠CDE，∴△ABG≌△CDE（ASA）；
（2）四边形EFGH是矩形．
证明：∵GA平分∠BAD，GB平分∠ABC，∴∠GAB=
∠BAD，∠GBA=
∠ABC，∵ABCD中，∠DAB+∠ABC=180°，∴∠GAB+∠GBA=
（∠DAB+∠ABC）=90°，即∠AGB=90°，同理可得，∠DEC=90°，∠AHD=90°=∠EHG，∴四边形EFGH是矩形；
（3）依题意得，∠BAG=
∠BAD=30°，∵AB=6，∴BG=
AB=3，AG=
=CE，∵BC=4，∠BCF=
∠BCD=30°，∴BF=
BC=2，CF=
，∴EF=
﹣
=
，GF=3﹣2=1，∴矩形EFGH的面积=EF×GF=
．
