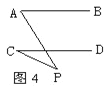
题目内容
【题目】已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.

【答案】证明见解析
【解析】证明:(1)连接AM,

∵△ABC是等边三角形,∴∠B=∠BAC=60°。
∴∠KAC=180°﹣∠BAC=120°。
∵⊙M与BA的延长线AK及边AC均相切,
∴∠KAM=∠CAM=![]() ∠KAC=
∠KAC=![]() ×120°=60°。
×120°=60°。
∴∠KAM=∠B=60°。∴AM∥BC。
(2)∵△ABC是等边三角形,∴∠B=∠BAC=∠ACB=60°。
∴∠KAC=180°﹣∠BAC=120°,∠FCA=120°。
∵⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,
∴∠KAM=∠CAM=![]() ∠KAC=
∠KAC=![]() ×120°=60°,
×120°=60°,
∠FCM=∠ACM=![]() ∠FCA=
∠FCA=![]() ×120°=60°。
×120°=60°。
∴∠KAM=∠B=60°,∠FCM=∠B=60°。
∴AM∥BC,CM∥AB,∴四边形ABCM是平行四边形。
(1)由等边△ABC,即可得∠B=∠BAC=60°,求得∠KAC=120°,又由⊙M与BA的延长线AK及边AC均相切,利用切线长定理,即可得∠KAM=60°,然后根据同位角相等,两直线平行,证得AM∥BC。
(2)根据(1),易证得AM∥BC,CM∥AB,从而可证得四边形ABCM是平行四边形。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目