��Ŀ����
����Ŀ�����ų��л�����ķ�չ����ͨӵ�³�Ϊ�ϰ�߷�ʱ���Ա��������Ϊ�˽���Ȫ��ij����·��ͨӵ���������Ȫij��ѧͬѧ��ʵ��ͳ�Ʒ����о���������![]() ʱ�������ٶ�v��ǧ��/Сʱ���dz����ܶ�x����/ǧ�ף���һ�κ��������õ�·�ij����ܶȴﵽ220��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶ�Ϊ95��/ǧ��ʱ�������ٶ�Ϊ50ǧ��/Сʱ��
ʱ�������ٶ�v��ǧ��/Сʱ���dz����ܶ�x����/ǧ�ף���һ�κ��������õ�·�ij����ܶȴﵽ220��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶ�Ϊ95��/ǧ��ʱ�������ٶ�Ϊ50ǧ��/Сʱ��
��1����![]() ʱ�������ٶ�v��ǧ��/Сʱ���복���ܶ�x����/ǧ�ף��ĺ�����ϵʽ��
ʱ�������ٶ�v��ǧ��/Сʱ���복���ܶ�x����/ǧ�ף��ĺ�����ϵʽ��
��2��Ϊʹ�õ�·�ϳ����ٶȴ���40ǧ��/Сʱ��С��60ǧ��/Сʱ��Ӧ���Ƹõ�·�ϵij����ܶ���ʲô��Χ�ڣ�
��3������������/Сʱ���ǵ�λʱ����ͨ���õ�·��ij�۲��ij�����������������=�����ٶȡ������ܶȣ���![]() ʱ����õ�·�ϳ�����y�����ֵ����ʱ�����ٶ�Ϊ���٣�
ʱ����õ�·�ϳ�����y�����ֵ����ʱ�����ٶ�Ϊ���٣�
���𰸡���1��v����![]() x+88����2��70��x��120����3��������y�����ֵ��ÿСʱ4840������ʱ�����ٶ���44ǧ��/ʱ��
x+88����2��70��x��120����3��������y�����ֵ��ÿСʱ4840������ʱ�����ٶ���44ǧ��/ʱ��
��������
��1����20��x��220ʱ���賵���ٶ�v�복���ܶ�x�ĺ�����ϵʽΪv��kx+b���ٸ��ݴ���ϵ������⼴�ɣ�
��2���ɣ�1���Ľ���ʽ��������ʽ�������⼯���ɣ�
��3���賵����y��x֮��Ĺ�ϵʽΪy��vx����20��x��220ʱ��ʾ����Ӧ�Ķ��κ�����ϵ���ɶ��κ��������ʾͿ�����������
�⣺��1���賵���ٶ�v�복���ܶ�x�ĺ�����ϵʽΪv��kx+b�������⣬��
![]() ����ã�
����ã�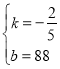 ��
��
�൱20��x��220ʱ��v����![]() x+88��
x+88��
��2�������⣬�ã� ����ã�70��x��120��
����ã�70��x��120��
��Ӧ���Ƹõ�·�ϵij����ܶ���70��x��120��Χ�ڣ�
��3���賵����y��x֮��Ĺ�ϵʽΪy��vx��
��20��x��220ʱ��y������![]() x+88��x����
x+88��x����![]() ��x��110��2+4840��
��x��110��2+4840��
�൱x��110ʱ��y���4840����ʱ![]() ǧ��/ʱ��
ǧ��/ʱ��
�൱�����ܶ���110��/ǧ��ʱ��������yȡ�����ֵ��ÿСʱ4840������ʱ�����ٶ���44ǧ��/ʱ��

����Ŀ����һ�������Ŀڴ���װ��ֻ����ɫ��ͬ�ĺڡ���������ɫ����5ֻ��ijѧϰС��������ʵ�飬������Ⱥ�����������һ���������ɫ���ٰ����Żش��У������ظ����±��ǻ�����е�һ��ͳ�����ݣ�
����Ĵ��� n | 100 | 150 | 200 | 500 | 800 | 1000 |
��������Ĵ��� m | 58 | 96 | 116 | 295 | 484 | 601 |
���������Ƶ�� | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
��1������ƣ���n�ܴ�ʱ�����������Ƶ�ʽ���ӽ��� �������ȷ��0.1����
��2���Թ���ڴ��к������� ֻ���������� ֻ��
��3���ڣ�2���Ľ����£��������б�����״ͼ�����������������ǰ���ĸ��ʣ�