题目内容
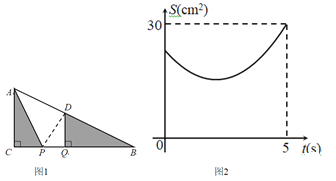
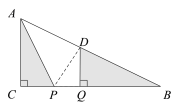
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm.点P、Q是BC边上两个动点(点Q在点P右边),PQ=2cm,点P从点C出发,沿CB向右运动,运动时间为t秒.5s后点Q到达点B,点P、Q停止运动,过点Q作QD⊥BC交AB于点D,连接AP,设△ACP与△BQD的面积和为S(cm),S与t的函数图像如图2所示.
(1)图1中BC= cm,点P运动的速度为 cm/s;
(2)t为何值时,面积和S最小,并求出最小值;
(3)连接PD,以点P为圆心线段PD的长为半径作⊙P,当⊙P与![]() 的边相切时,求t的值.
的边相切时,求t的值.
【答案】(1)12 , 2;(2)当t=2时,面积和S最小,最小为21cm2. (3)当t=1或![]() 时⊙P与△ABC的边相切
时⊙P与△ABC的边相切
【解析】
(1)根据题意知,点Q与点B重合时,△ACP的面积为30,依据三角形面积公式可得PC的长为10,由PQ=2得BC的长为12,根据“速度=路程÷时间”可求出点P的速度;
(2)分别求出PC=2t,BQ=10-2t,DQ=5-t,利用三角形面积公式得到二次函数关系式,进行配方即可求出最值;
(3)分⊙P与AB边和AC边相切两种情况进行分类讨论求解即可.
(1)当点Q与点B重合时,△ACP的面积=30,
∴![]()
∵AC=6cm,
∴PC=10cm,
∴BC=PC+PQ=10+2=12cm,
∴点P的速度为:10÷5=2(cm/s);
(2)由题可知PC=2t,BQ=12-2-2t=10-2t,
∵DQ⊥BC,AC⊥BC,
∴DQ∥AC,
∴△DQB∽△ACB,
∴![]() ,即
,即![]()
∴DQ=5-t
∴S=![]() =
=![]()
∴当t=2时,面积和S最小,最小为21cm2.
(3)⊙P与BC边不可能相切
i) ⊙P与AB边相切时△PQD∽△ACB,![]()
∴![]() ,
,
∴t=1
ii)⊙P与AC边相切时![]()
在Rt△PQD中,![]() ,
,
∴![]()
∴t=![]() 或t=
或t=![]() (舍去),
(舍去),
综上当t=1或![]() 时⊙P与△ABC的边相切.
时⊙P与△ABC的边相切.

【题目】为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
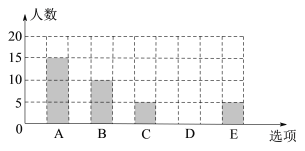
根据以上信息回答下列问题:
(1)这次调查的样本容量是 ;
(2)统计表中m= ,n= ,补全条形统计图;
(3)若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.