题目内容
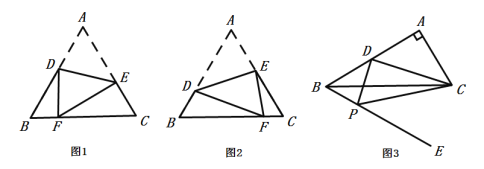
【题目】(1)如图1,△ABC为等边三角形,点D、E分别为边AB、AC上的一点,将图形沿线段DE所在的直线翻折,使点A落在BC边上的点F处求证:![]() ;
;
(2)如图2,按图1的翻折方式,若等边△ABC的边长为4,当![]() 时,求
时,求![]() 的值;
的值;
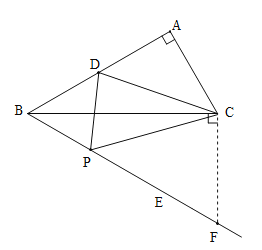
(3)如图3,在![]() 中,
中,![]() ,点D是AB边上的中点,在BC的下方作射线BE,使得
,点D是AB边上的中点,在BC的下方作射线BE,使得![]() ,点P是射线BE上一个动点,当
,点P是射线BE上一个动点,当![]() ,求BP的长.
,求BP的长.
【答案】(1)见解析;(2)![]() ;(3)2或6
;(3)2或6
【解析】
(1)根据三角形外角的性质证明∠BDF=∠EFC,从而可得△BDF∽△CFE,根据相似三角形对应边成比例即可得出结论;
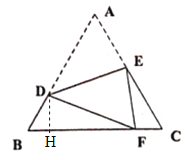
(2)过D作DH⊥BC.设BF=x,则CF=4-x.设EF=2a,则DF=3a,AE=2a,BD=4-AD=4-3a,CE=4-AE=4-2a,由相似三角形对应边成比例,即可得出x、a的值,从而求得BD、DF、DH的长,根据正弦的定义即可得出结论;
(3)解Rt△ABC得到BC、AB、BD的长.过C作CF⊥BC,交BE于F,解Rt△BCF,得到CF、BF的长.通过证明△DBPΔPFC,由相似三角形对应边成比例即可得出结论.
(1)![]() ,
,
又![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.
(2)过D作![]() .
.
设![]() ,则
,则![]() .
.
设![]() ,则
,则![]() ,AE=2a,
,AE=2a,
![]() ,
,
![]() .
.
由(1)知![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
(3)∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.
过C作![]() ,交BE于F.
,交BE于F.
∵∠CBF=30°,
∴![]() CF=BC=
CF=BC=![]() ,
,
∴CF=4,∴BF=2CF=8.
∵![]()
![]() ,
,
![]() .
.
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 或6.
或6.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案【题目】小明同学利用寒假30天时间贩卖草莓,了解到某品种草莓成本为10元/千克,在第![]() 天的销售量与销售单价如下(每天内单价和销售量保持一致):
天的销售量与销售单价如下(每天内单价和销售量保持一致):
销售量 |
|
销售单价 | 当 |
当 |
设第![]() 天的利润
天的利润![]() 元.
元.
(1)请计算第几天该品种草莓的销售单价为25元/千克?
(2)这30天中,该同学第几天获得的利润最大?最大利润是多少?注:利润=(售价-成本)×销售量
【题目】为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
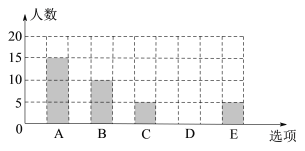
根据以上信息回答下列问题:
(1)这次调查的样本容量是 ;
(2)统计表中m= ,n= ,补全条形统计图;
(3)若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.