Question

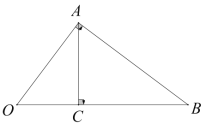
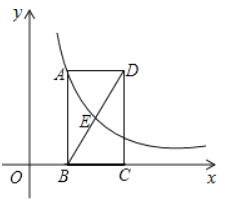
【题目】如图，已知点在函数的图象上，矩形的边在轴上，是对角线的中点，函数的图象经过两点，点的横坐标为，点的横坐标为，解答下列问题：

（1）求反比例函数的解析式；

（2）求点的坐标（用表示）；

（3）当时，求的值．

Answer 1

【答案】（1）；（2）；（3）．

【解析】

（1）把代入反比例函数解析式即可；

（2）设点横坐标为，得出纵坐标为：，根据是中点，得出的纵坐标为进而求出的横坐标：，所以得出的横坐标：，根据，得出，从而求出的坐标；

（3）时，，把（2）中的代数式代入即可求解．

（1）点在函数的图象上，

将点代入，则，

解得，

反比例函数解析式为；

（2）设点横坐标为，

点在函数上，

点坐标为，

则点的纵坐标为，

点在函数上，

点坐标为，

则点横坐标为，

，

，，

点坐标为；

（3），

即，

，

舍去，