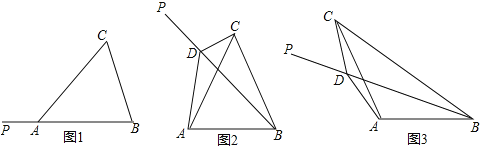
��Ŀ����
����Ŀ���ڡ�ABC�У�AB=AC����F��BC�ӳ�����һ�㣬��CFΪ�ߣ�������CDEF��ʹ����CDEF���A��BC��ͬ�࣬����BE����G��BE���е㣬����AG��DG��
��1����ͼ�٣�����BAC=��DCF=90��ʱ��ֱ��д��AG��DG��λ�ú�������ϵ��
��2����ͼ�ڣ�����BAC=��DCF=60��ʱ����̽��AG��DG��λ�ú�������ϵ��
��3������BAC=��DCF=��ʱ��ֱ��д��AG��DG��������ϵ��

���𰸡���1��AG��DG��AG=DG����2��AG��GD��AG=![]() DG����3��DG=AGtan
DG����3��DG=AGtan![]() ��
��
��������
�����������1���ӳ�DG��BC����H������AH��AD����֤��BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC����֤��ABH�ա�ACD���ó���BAH=��CAD��AH=AD�����������HAD=90�㣬�������AG��GD��AG=GD��
��2���ӳ�DG��BC����H������AH��AD����֤��BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC����֤��ABH�ա�ACD���ó���BAH=��CAD��AH=AD�����������HAD�ǵȱ������Σ�����֤��AG��GD��AG=![]() DG��
DG��
��3���ӳ�DG��BC����H������AH��AD����֤��BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC����֤��ABH�ա�ACD���ó���BAH=��CAD��AH=AD�����������HAD�ǵ��������Σ�����֤��DG=AGtan![]() ��
��
�����������1��AG��DG��AG=DG��֤�����£��ӳ�DG��BC����H������AH��AD�����ı���DCEF�������Σ���DE=DC��DE��CF�����GBH=��GED����GHB=��GDE����G��BC���е㣬��BG=EG������BGH����EGD�����ߡ�GBH=��GED����GHB=��GDE��BG=EG�����BGH�ա�EGD��AAS������BH=ED��HG=DG����BH=DC����AB=AC����BAC=90�㣬���ABC=��ACB=45�㣬�ߡ�DCF=90�㣬���DCB=90�㣬���ACD=45�㣬���ABH=��ACD=45�㣬����ABH����ACD������AB=AC����ABH=��ACD��BH=CD�����ABH�ա�ACD��SAS�������BAH=��CAD��AH=AD���ߡ�BAH+��HAC=90�㣬���CAD+��HAC=90�㣬����HAD=90�㣬��AG��GD��AG=GD��
��2��AG��GD��AG=![]() DG��֤�����£��ӳ�DG��BC����H������AH��AD�����ı���DCEF�������Σ���DE=DC��DE��CF�����GBH=��GED����GHB=��GDE����G��BC���е㣬��BG=EG������BGH����EGD�����ߡ�GBH=��GED����GHB=��GDE��BG=EG�����BGH�ա�EGD��AAS������BH=ED��HG=DG����BH=DC����AB=AC����BAC=��DCF=60�����ABC=60�㣬��ACD=60�㣬���ABC=��ACD=60�㣬����ABH����ACD������AB=AC����ABH=��ACD��BH=CD�����ABH�ա�ACD��SAS�������BAH=��CAD��AH=AD�����BAC=��HAD=60������AG��HD����HAG=��DAG=30�㣬��tan��DAG=tan30��=
DG��֤�����£��ӳ�DG��BC����H������AH��AD�����ı���DCEF�������Σ���DE=DC��DE��CF�����GBH=��GED����GHB=��GDE����G��BC���е㣬��BG=EG������BGH����EGD�����ߡ�GBH=��GED����GHB=��GDE��BG=EG�����BGH�ա�EGD��AAS������BH=ED��HG=DG����BH=DC����AB=AC����BAC=��DCF=60�����ABC=60�㣬��ACD=60�㣬���ABC=��ACD=60�㣬����ABH����ACD������AB=AC����ABH=��ACD��BH=CD�����ABH�ա�ACD��SAS�������BAH=��CAD��AH=AD�����BAC=��HAD=60������AG��HD����HAG=��DAG=30�㣬��tan��DAG=tan30��=![]() ����AG=
����AG=![]() DG��
DG��
��3��DG=AGtan![]() ��֤�����£��ӳ�DG��BC����H������AH��AD�����ı���DCEF�������Σ���DE=DC��DE��CF�����GBH=��GED����GHB=��GDE����G��BC���е㣬��BG=EG������BGH����EGD������GBH=��GED����GHB=��GDE��BG=EG�����BGH�ա�EGD��AAS������BH=ED��HG=DG����BH=DC����AB=AC����BAC=��DCF=�������ABC=90�㩁
��֤�����£��ӳ�DG��BC����H������AH��AD�����ı���DCEF�������Σ���DE=DC��DE��CF�����GBH=��GED����GHB=��GDE����G��BC���е㣬��BG=EG������BGH����EGD������GBH=��GED����GHB=��GDE��BG=EG�����BGH�ա�EGD��AAS������BH=ED��HG=DG����BH=DC����AB=AC����BAC=��DCF=�������ABC=90�㩁![]() ����ACD=90�㩁
����ACD=90�㩁![]() �����ABC=��ACD������ABH����ACD����AB=AC����ABH=��ACD��BH=CD�����ABH�ա�ACD��SAS�������BAH=��CAD��AH=AD�����BAC=��HAD=������AG��HD����HAG=��DAG=
�����ABC=��ACD������ABH����ACD����AB=AC����ABH=��ACD��BH=CD�����ABH�ա�ACD��SAS�������BAH=��CAD��AH=AD�����BAC=��HAD=������AG��HD����HAG=��DAG=![]() ����tan��DAG=tan
����tan��DAG=tan![]() =
=![]() ����DG=AGtan
����DG=AGtan![]() ��
��


 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�