题目内容
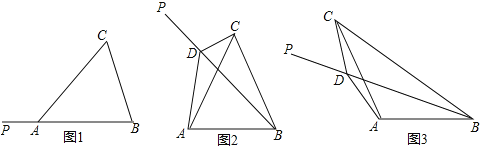
【题目】如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
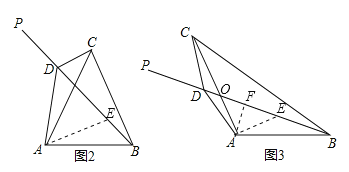
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
【答案】(1)=,BD=CD+AD;(2)证明见试题解析;(3)BD+CD=![]() AD.
AD.
【解析】
试题分析:(1)如图2,由∠CDP=120°,得出∠CDB=60°,则∠CDB=∠BAC=60°,所以A、B、C、D四点共圆,由圆周角定理得出∠ACD=∠ABD;在BP上截取BE=CD,连接AE.利用SAS证明△DCA≌△EBA,得到AD=AE,∠DAC=∠EAB,再证明△ADE是等边三角形,得到DE=AD,进而得出BD=CD+AD.
(2)如图3,设AC与BD相交于点O,在BP上截取BE=CD,连接AE,过A作AF⊥BD于F.先证△DOC∽△AOB,得到∠DCA=∠EBA.再利用SAS证明△DCA≌△EBA,得到AD=AE,∠DAC=∠EAB.由∠CAB=∠CAE+∠EAB=120°,得出∠DAE=120°,由等腰三角形的性质及三角形内角和定理求出∠ADE=∠AED=30°.解Rt△ADF,得出DF=![]() AD,那么DE=2DF=
AD,那么DE=2DF=![]() AD,进而得出BD=DE+BE=
AD,进而得出BD=DE+BE=![]() AD+CD,即BD﹣CD=
AD+CD,即BD﹣CD=![]() AD;
AD;
(3)同(2)证明可以得出BD+CD=![]() AD.
AD.
试题解析:(1)如图2,∵∠CDP=120°,∴∠CDB=60°,∵∠BAC=60°,∴∠CDB=∠BAC=60°,∴A、B、C、D四点共圆,∴∠ACD=∠ABD.在BP上截取BE=CD,连接AE.在△DCA与△EBA中,∵AC=AB,∠ACD=∠ABE,CD=BE,∴△DCA≌△EBA(SAS),∴AD=AE,∠DAC=∠EAB,∵∠CAB=∠CAE+∠EAB=60°,∴∠DAE=60°,∴△ADE是等边三角形,∴DE=AD.∵BD=BE+DE,∴BD=CD+AD.故答案为:=,BD=CD+AD;
(2)如图3,设AC与BD相交于点O,在BP上截取BE=CD,连接AE,过A作AF⊥BD于F.
∵∠CDP=60°,∴∠CDB=120°.∵∠CAB=120°,∴∠CDB=∠CAB,∵∠DOC=∠AOB,∴△DOC∽△AOB,∴∠DCA=∠EBA.在△DCA与△EBA中,∵AC=AB,∠ACD=∠ABE,CD=BE,∴△DCA≌△EBA(SAS),∴AD=AE,∠DAC=∠EAB.∵∠CAB=∠CAE+∠EAB=120°,∴∠DAE=120°,∴∠ADE=∠AED=(180°-120°)÷2=30°.∵在Rt△ADF中,∠ADF=30°,∴DF=![]() AD,∴DE=2DF=
AD,∴DE=2DF=![]() AD,∴BD=DE+BE=
AD,∴BD=DE+BE=![]() AD+CD,∴BD﹣CD=
AD+CD,∴BD﹣CD=![]() AD;
AD;
(3)BD+CD=![]() AD.
AD.