��Ŀ����
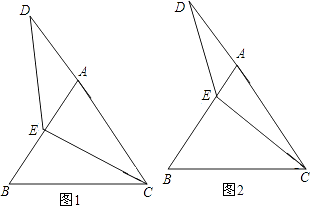
����Ŀ����ͼ1����������ABCD����࣬�������ȱ�������ADE��DCF������AF��BE��
��1�����жϣ�AF��BE��������ϵ�� ��λ�ù�ϵ�� ��
��2����ͼ2�����������������ȱ�������ADE��DCF����Ϊ����������������ADE��DCF����EA=ED=FD=FC�����ڣ�1�����еĽ����Ƿ���Ȼ�������������жϲ�����˵����
��3����������ADE��DCFΪһ�������Σ���AE=DF��ED=FC���ڣ�1�����еĽ��۶��ܳ�������ֱ��д������жϣ�

���𰸡���1����ȣ����ഹֱ����2����������3��������
��������
�����������1����֤��ADE�ա�DCF������֤��AF��BE��������ϵ�ǣ�AF=BE��λ�ù�ϵ�ǣ�AF��BE��
��2��֤����ADE�ա�DCF��Ȼ��֤����ABE�ա�ADF����֤��BE=AF��Ȼ������������ڽǺͶ���֤����AMB=90�㣬�Ӷ���֤��
��3���루2���Ľⷨ��ȫ��ͬ��
����������⣺��1��AF��BE��������ϵ�ǣ�AF=BE��λ�ù�ϵ�ǣ�AF��BE���ʴ�Ϊ����ȣ����ഹֱ��
��2��������Ȼ�����������ǣ���������ABCD�У�AB=AD=CD�����ڡ�ADE�͡�DCF�У���AE=DF��AD=CD��DE=CF�����ADE�ա�DCF�����DAE=��CDF������������ABCD�У���BAD=��ADC=90�㣬���BAE=��ADF�����ڡ�ABE�͡�ADF�У���AB=DA����BAE=��ADF��AE=DF�����ABE�ա�ADF����BE=AF����ABM=��DAF�����ߡ�DAF+��BAM=90�㣬���ABM+��BAM=90�㣬���ڡ�ABM�У���AMB=180�㩁����ABM+��BAM��=90�㣬��BE��AF��
��3���ڣ�1�����еĽ��۶��ܳ����������ǣ���������ABCD�У�AB=AD=CD�����ڡ�ADE�͡�DCF�У���AE=DF��AD=CD��DE=CF�����ADE�ա�DCF�����DAE=��CDF������������ABCD�У���BAD=��ADC=90�㣬���BAE=��ADF�����ڡ�ABE�͡�ADF�У���AB=DA����BAE=��ADF��AE=DF�����ABE�ա�ADF����BE=AF����ABM=��DAF�����ߡ�DAF+��BAM=90�㣬���ABM+��BAM=90�㣬���ڡ�ABM�У���AMB=180�㩁����ABM+��BAM��=90�㣬��BE��AF��