题目内容
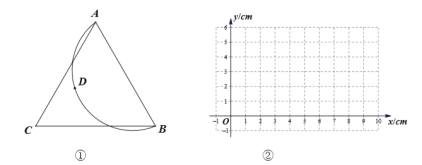
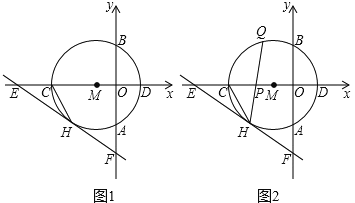
【题目】如图1所示,以点M(1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E(![]() ,0),交y轴于点F(0,
,0),交y轴于点F(0,![]() ).
).
(1)求⊙M的半径r;
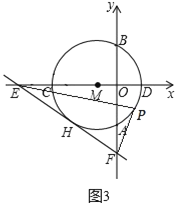
(2)如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC=![]() ,求
,求![]() 的值;
的值;
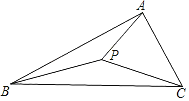
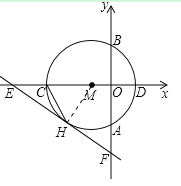
(3)如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+![]() PE的最小值.
PE的最小值.
【答案】(1)r=2;(2)![]() =
=![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接MH,根据点E(![]() ,0)和点F(0,
,0)和点F(0,![]() ),求出
),求出![]() 的值,再通过证明△EMH∽△EFO,得到
的值,再通过证明△EMH∽△EFO,得到![]() ,即可解出r的值;
,即可解出r的值;
(2)连接DQ、CQ,由cos∠QDC =cos∠QHC =![]() ,可得
,可得![]() ,由(1)可知,r=2,故CD=4,由DQ=3,CH是RT△EHM斜边上的中线,得到CH=
,由(1)可知,r=2,故CD=4,由DQ=3,CH是RT△EHM斜边上的中线,得到CH=![]() EM=2.再通过证明△CHP∽△QDP,即可得到
EM=2.再通过证明△CHP∽△QDP,即可得到![]() ;
;
(3)取CM的中点N,连接PM、PN,由OM=1,OE=5,可得ME=4,进而得到![]() ,
,
通过证明△PMN∽△EMP,可得![]() ,即
,即![]() ,所以当F、P、N三点共线时,PF+
,所以当F、P、N三点共线时,PF+![]() PE的最小值为FN的长,根据勾股定理可求的PF+
PE的最小值为FN的长,根据勾股定理可求的PF+![]() PE的最小值.
PE的最小值.
(1)如图,连接MH,
∵点E(![]() ,0)和点F(0,
,0)和点F(0,![]() ),
),
∴OE=5,OF=![]() ,
,
∴![]() ,
,
∵M(-1,0),
∴OM=1,
∴EM=OE-OM=4,
∵∠E=∠E,∠AOE=∠EHM,
∴△EMH∽△EFO,
∴![]() ,
,
即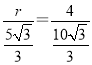 ,
,
∴r=2;
(2) 如图,连接DQ、CQ.
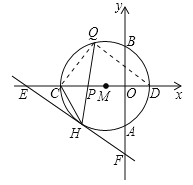
∵CD为直径,∴∠CQD=90°,
∵∠QHC=∠QDC,
∴cos∠QDC =cos∠QHC =![]() ,
,
∴![]() ,
,
由(1)可知,r=2,故CD=4,
∴DQ=3,
∵CH是RT△EHM斜边上的中线,
∴CH=![]() EM=2.
EM=2.
∵∠CHP=∠QDP,∠CPH=∠QPD,
∴△CHP∽△QDP,
∴![]() ;
;
(3)如图,取CM的中点N,连接PM、PN,
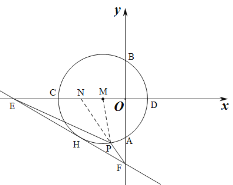
∵OM=1,OE=5,
∴ME=4,
∴![]() ,
,
又∵∠PMN=∠EMP,
∴△PMN∽△EMP,
∴![]() ,
,
∴![]() ,
,
当F、P、N三点共线时,PF+![]() PE的最小值为FN的长,
PE的最小值为FN的长,
∴点N为CM的中点,
∴ON=2,
∴![]() ,
,
∴PF+![]() PE的最小值为
PE的最小值为![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案