题目内容
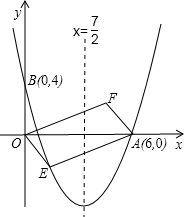
如图,抛物线y=ax2-
x+2与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
(1)求a的值和抛物线的顶点坐标;
(2)分别连接AC、BC.在x轴下方的抛物线上求一点M,使△AMC与△ABC的面积相等;
(3)设N是抛物线对称轴上的一个动点,d=|AN-CN|.探究:是否存在一点N,使d的值最大?若存在,请直接写出点N的坐标和d的最大值;若不存在,请简单说明理由.

| 1 |
| 3 |
(1)求a的值和抛物线的顶点坐标;
(2)分别连接AC、BC.在x轴下方的抛物线上求一点M,使△AMC与△ABC的面积相等;
(3)设N是抛物线对称轴上的一个动点,d=|AN-CN|.探究:是否存在一点N,使d的值最大?若存在,请直接写出点N的坐标和d的最大值;若不存在,请简单说明理由.

(1)∵抛物线y=ax2-
x+2经过点B(3,0),
∴9a-
×3+2=0,
解得a=-
,
∴y=-
x2-
x+2,
∵y=-
x2-
x+2=-
(x2+3x)+2=-
(x+
)2+
,
∴顶点坐标为(-
,
);
(2)∵抛物线y=-
x2-
x+2的对称轴为直线x=-
,
与x轴交于点A和点B,点B的坐标为(3,0),
∴点A的坐标为(-6,0).
又∵当x=0时,y=2,
∴C点坐标为(0,2).
设直线AC的解析式为y=kx+b,
则
,解得
,
∴直线AC的解析式为y=
x+2.
∵S△AMC=S△ABC,
∴点B与点M到AC的距离相等,
又∵点B与点M都在AC的下方,
∴BM∥AC,
设直线BM的解析式为y=
x+n,
将点B(3,0)代入,得
×3+n=0,
解得n=-1,
∴直线BM的解析式为y=
x-1.
 由
由
,解得
,
,
∴M点的坐标是(-9,-4);
(3)在抛物线对称轴上存在一点N,能够使d=|AN-CN|的值最大.理由如下:
∵抛物线y=-
x2-
x+2与x轴交于点A和点B,
∴点A和点B关于抛物线的对称轴对称.
连接BC并延长,交直线x=-
于点N,连接AN,则AN=BN,此时d=|AN-CN|=|BN-CN|=BC最大.
设直线BC的解析式为y=mx+t,将B(3,0),C(0,2)两点的坐标代入,
得
,
,
∴直线BC的解析式为y=-
x+2,
当x=-
时,y=-
×(-
)+2=3,
∴点N的坐标为(-
,3),d的最大值为BC=
=
.
| 1 |
| 3 |
∴9a-
| 1 |
| 3 |
解得a=-
| 1 |
| 9 |
∴y=-
| 1 |
| 9 |
| 1 |
| 3 |
∵y=-
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
| 3 |
| 2 |
| 9 |
| 4 |
∴顶点坐标为(-
| 3 |
| 2 |
| 9 |
| 4 |
(2)∵抛物线y=-
| 1 |
| 9 |
| 1 |
| 3 |
| 3 |
| 2 |
与x轴交于点A和点B,点B的坐标为(3,0),
∴点A的坐标为(-6,0).
又∵当x=0时,y=2,
∴C点坐标为(0,2).
设直线AC的解析式为y=kx+b,
则
|
|
∴直线AC的解析式为y=
| 1 |
| 3 |
∵S△AMC=S△ABC,
∴点B与点M到AC的距离相等,
又∵点B与点M都在AC的下方,
∴BM∥AC,
设直线BM的解析式为y=
| 1 |
| 3 |
将点B(3,0)代入,得
| 1 |
| 3 |
解得n=-1,
∴直线BM的解析式为y=
| 1 |
| 3 |
 由
由
|
|
|
∴M点的坐标是(-9,-4);
(3)在抛物线对称轴上存在一点N,能够使d=|AN-CN|的值最大.理由如下:
∵抛物线y=-
| 1 |
| 9 |
| 1 |
| 3 |
∴点A和点B关于抛物线的对称轴对称.
连接BC并延长,交直线x=-
| 3 |
| 2 |
设直线BC的解析式为y=mx+t,将B(3,0),C(0,2)两点的坐标代入,
得
|
|
∴直线BC的解析式为y=-
| 2 |
| 3 |
当x=-
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
∴点N的坐标为(-
| 3 |
| 2 |
| 32+22 |
| 13 |

练习册系列答案
相关题目




 大?
大?